Il padre putativo della geometria frattale, il matematico Benoit Mandelbrot, è stato un padre moderno. Morto solo nel 2010, ricevette il premio Wolf per la fisica nel 1993 per “aver trasformato la nostra visione della natura“. Il suo lavoro pioneristico ha posto le basi a sostegno di una visione unificata di diversi fenomeni naturali. La teoria frattale è esplosa in un periodo, gli anni ’70, molto proficuo per la ricerca scientifica. Per tutto il suo sviluppo ha spesso intersecato la strada di altri campi di ricerca, spaziando trasversalmente dalla teoria del gruppo di rinormalizzazione, passando per medicina e biologia, fino a raggiungere la teoria di caos deterministico.
Il termine frattale stesso è stato per la prima volta assegnato da Mandelbrot nel libro: “Les Objects Fractals: Forme, Hazard et Dimension”, pubblicato nel 1975. Durante la assegnazione della laurea honoris causa in Medicina e Chirurgia, conferitagli dall’Università degli studi di Bari nel 2007, dichiarò:
Il concetto di base che unisce lo studio dei frattali alle discipline come la biologia e quindi anatomia e fisiologia parte dalla convinzione di un necessario superamento della geometria euclidea nella descrizione della realtà naturale. Volendo essere molto sintetici, i frattali servono a trovare una nuova rappresentazione che parta dall’idea di base che il piccolo in natura non è nient’altro che una copia del grande. La mia convinzione è che i frattali saranno presto impiegati nella comprensione dei processi neurali, la mente umana sarà la loro nuova frontiera.
Mandelbrot insegna a diffidare del senso comune. E’ erroneo pensare che, una volta ridotta all’osso, la natura si esprima attraverso elementi di geometria euclidea (linee, cerchi ecc..), per le quali si è costruito nei secoli un ricco apparato matematico in grado di risolvere analiticamente un qualsiasi problema geometrico attraverso l’analisi differenziale. Quando ancora la teoria frattale non era stata introdotta formalmente, nonostante fossero però ben noti i lavori descrittivi di alcuni oggetti facenti parti la categoria ad opera di celebri matematici del passato (Cantor, Peano, Hilbert, Sierpinski.. ), Mandelbrot, prendendo spunto da questi, ha sviluppato una teoria geometrica nuova e necessaria in risposta al fatto che quasi mai è possibile approssimare linearmente fenomeni naturali.
L’invarianza di scala che contraddistingue gli insiemi frattali comporta caratteristiche di intrinseca irregolarità che non possono essere descritte con i metodi matematici tradizionali.
Quando una struttura viene caratterizzata in modo naturale da una legge di potenza con esponente non intero, dal punto di vista matematico, questo comportamento è appunto non analitico e la non analiticità è una delle caratteristiche dei frattali. Se c’è una cosa le scienze insegnano è che la natura non è perfetta. Figure semplici come la sfera sono platoniche, la realtà devia dalla perfezione. La matematica da sola ci racconta di un mondo ideale, perfetto. La fisica adatta questo racconto alla vera realtà introducendo forze dissipative, fenomeni stocastici, principi di indeterminazione ecc… Sotto questo punto di vista riconoscere la natura frattale delle cose è quasi banale. Basti pensare alle nuvole in cielo, ai confini naturali delle nazioni, al pattern dei fulmini e vasi sanguigni, alle felci e ai fiori, alle montagne. Anche processi di selezione naturale e andamenti delle azioni nei mercati finanziari hanno un andamento frattale.
Essendo così diffusa in tutta la natura, è utile studiare quelle che sono le regolarità ricorrenti in tali oggetti a prima vista molto irregolari. Un esempio, il più semplice ed esplicativo possibile, della regolarità celata dietro ad una apparenza a dir poco caotica riguarda il moto browniano, un moto incessante e irregolare la cui traiettoria rientra a tutti gli effetti nella definizione di frattale stocastico. Per saperne di più basta cliccare proprio qui. Quel che segue sono alcune nozioni utili al fine di poter comprendere meglio questi curiosi oggetti.
Dimensionalità
Per prima cosa è bene togliersi ogni dubbio su cosa sia un frattale e, quindi, su che cosa si intenda per dimensione frattale poiché, la sua definizione, è strettamente legata al concetto di “dimensione” di un insieme. Su questo lo stesso Mandelbrot sembra essere indeciso poiché nei suoi lavori impiega tre diverse definizioni del termine frattale. Egli considera, equivalentemente, un frattale:
- Un oggetto dalla forma frammentata, spezzata e altamente discontinua. Un oggetto cioè dotato di una intrinseca regolarità
- Un oggetto fatto di parti che sono in qualche modo simili al tutto. In termini più rigorosi, il frattale deve presentare proprietà di autosimilarità, deve cioè ripetersi uguale a tutte le scale di osservazione. Nella realtà questa proprietà è distorta, va intesa più in senso statistico, ma ne riparleremo più tardi
- Un insieme per il quale la sua dimensione di Hausdorf sia maggiore della sua dimensione topologica

Intuitivamente ci si trova d’accordo con le prime due definizioni. Se prendo come esempio la figura a lato, riconosco immediatamente che l’oggetto rappresentato è un frattale per il quale sia la prima che la seconda definizione calzano a pennello. Tuttavia, esse risultano insufficienti quando si tratta di specificare rigorosamente un frattale. Serve una definizione più rigorosa – la numero 3. Normalmente quando si parla di dimensione, si sottintende la dimensione topologica. Se prendo come riferimento una curva, una superficie o un volume qualsiasi, per identificarne la posizione di un punto sulla figura, quello che faccio è considerare una corrispondenza biunivoca e continua fra le coordinate necessarie alla sua identificazione e la retta reale. Se ho una linea la coordinata necessaria è una, se ho una superficie ho bisogno di due coordinate, per un volume tre. Il suffisso topologica si riferisce al fatto che uso le proprietà topologiche d’insieme (continuità e relazione di biunivocità) per definire la dimensione dell’oggetto. Se voglio specificare un oggetto per mezzo della sua dimensione frattale, detta dimensione di Hausdorf, invece, faccio uso della dimensione metrica d’insieme poiché è attraverso la procedura di misurazione che ne identifico la dimensione.
E’ la dimensione metrica, basata sulla misura di un insieme, quella utilizzata per riconoscere se un oggetto è frattale o meno, non la dimensione topologica basata invece sulla corrispondenza biunivoca e continua fra la retta reale e le coordinate necessarie a identificare l’oggetto.
Posso pensare di misurare una corda di lunghezza totale L attraverso l’impiego di una spezzata di lunghezza l (con $l<L$)e indicare con N il numero delle spezzate necessarie a coprire la lunghezza della corda L. Se la corda è lunga 1m e la spezzata 10cm, saranno necessarie 10 spezzate per ricoprire l’intera corda. Se la spezzata è lunga 50cm allora me ne serviranno solo due. Quindi, data una lunghezza fissa L, $N \sim \frac{1}{l}$. Lo stesso dicasi per una superficie il cui ricoprimento andrà come $N \sim \frac{1}{l^2}$ e un volume con ricoprimento che va come $N \sim \frac{1}{l^3}$.
$N$ ed $l$ sono inversamente proporzionali tra loro. Gli esempi citati sono decisamente banali, e la relazione inversa presente fra il numero di ricoprimenti e la loro grandezza appare ovvia, ma cosa accadrebbe se la potenza cui si elevasse l’esponente $l$ non fosse intera?
Mandelbrot si è tenuto alla larga dalle dimensioni intere per addentrarsi nel mondo delle dimensioni non intere. In seguito alle sue ricerche poi, molti matematici hanno abbandonato l’ambito della geometria ed hanno affrontato il problema dei frattali stocastici, ma di questo parleremo più tardi.
Insieme triadico di von Koch
Capire appieno quel che comporta l’introduzione di un esponente frazionario permette di rispondere alla domanda che inizialmente si era posto il fisico-matematico Lewis Fry Richardson nella sua ricerca di una relazione fra la lunghezza dei confini fra due nazioni e la loro probabilità di entrare in guerra: “Quanto misura la costa dell’Inghilterra?”. Su questo interrogativo Mandelbrot scrisse nel ’69 un articolo dal titolo “How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension“, a cui rimando tramite link.
Ora, nulla è più esplicativo di un esempio. A questo proposito, prendo come primo riferimento di una ricopertura di insieme che segue una legge di potenza con esponente frazionario il triangolo di Von Koch. Esso si ottiene:
- Tracciando un segmento rettilineo e dividendolo in tre parti uguali
- Rimuovendo la parte centrale
- Andandola a sostituire con un triangolo equilatero di lato pari alla spezzata rimossa
- Ripetendo all’infinito il procedimento per ogni sotto-segmento
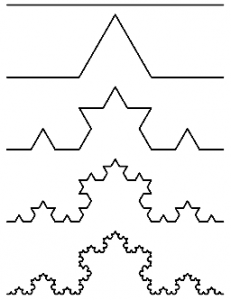
Topologicamente non vi è differenza fra la dimensione di questo oggetto e quella di un’altra curva qualsiasi, metricamente, invece, si. Provo a spiegarmi meglio, ripetendo il procedimento di misura precedente per evidenziarne la differenza. Indico con L la lunghezza totale della curva di von Koch, N il numero delle spezzate necessarie a ricoprirla e l la loro lunghezza, tale che:
$$ L = N \times l, \ con \ a = \frac{1}{l} = risoluzione$$
Come fare a scegliere il giusto passo l? Se è fosse troppo grande, la misura sarebbe insensibile alle piccole variazioni, viceversa lo sarebbe troppo e potrebbe tendere “idealmente” all’infinito. Secondo Hausdorf e Besicovitch la definizione operativa di dimensione è intesa come: quel numero critico D, se esiste ed è finito, per cui la misura passa da valere 0 a valere infinito.
Qual è il valore della misura metrica d’insieme D? Iterando il procedimento, la relazione che si ottiene è: $L=\frac{4}{3}^n$. Indico con d la dimensione topologica. Allora:
$$M=\sum l^{d}=4^{n} \cdot 3^{-nd}$$ con $n= – \frac{log(l)}{log(3)}$
| passo (n) | numero spezzate (N) | lunghezza spezzate (l) | lunghezza totale (L) |
|---|---|---|---|
| n=1 | N=$4^1$=4 | l=$\frac{1}{3}^1$=$\frac{1}{3}$ | L=$\frac{4}{3}$ |
| n=2 | N=$4^2$=16 | l=$\frac{1}{3}^2$=$\frac{1}{9}$ | L=$\frac{16}{9}$=$\frac{4}{3}$ |
| n=3 | N=$4^3$=64 | l=$\frac{1}{3}^3$=$\frac{1}{27}$ | L=$\frac{64}{27}$ |
$$M=exp[n log(4)- nd log(3)] = exp[n \cdot (log(4)-d log(3))] =$$
$$= exp[(-\frac{log(l)}{log(3)})\cdot (log(4)-d log(3))]= exp[log(l) \cdot (d – \frac{log(4)}{log(3)})]=l^{(d-\frac{log(4)}{log(3)})}$$
$\displaystyle \lim_{ l \to 0} M = 0 \ se \ d>\frac{log(4)}{log(3)}$
$\displaystyle \lim_{ l \to 0} M = \infty \ se \ d<\frac{log(4)}{log(3)}$
Allora $$D= \frac{log(4)}{log(3)} = 1.2628, \ L = l^{1-D}$$
La dimensione metrica della curva di von Koch è quindi frattale, non intera. SI dice essere più di una linea e meno di una superficie.
In realtà Mandelbrot chiama queste curve con n frazionario ma comunque finito, curve pre-frattali poiché possono essere stirate per formare una retta.
Insieme triadico di Cantor
- Si traccia un segmento rettilineo e lo si divide in tre parti uguali
- Si rimuove interamente la parte centrale
- Si ripete all’infinito il procedimento. Quel che si ottiene è nota come polvere di Cantor.

Anche in questo caso l’iniziatore è un segmento di retta, ma diversamente dall’insieme di von Koch la dimensione di Hausdorf è inferiore alla unità e per questo viene detto ad esso complementare. Il generatore, invece, prevede la rimozione del terzo centrale all’iniziatore mentre nella procedura di von Koch vi è una vera e propria sostituzione di questo elemento.
$$M = {N l}^d = 2^n \cdot \frac{1}{3}^{nd}$$
con $n = – \frac{log(l)}{log(3)}$
| passo (n) | numero spezzate (N) | lunghezza spezzate (l) | lunghezza totale (L) |
|---|---|---|---|
| n=1 | N=$2^1$=2 | l=$\frac{1}{3}^1$=$\frac{1}{3}$ | L=$\frac{2}{3}$ |
| n=2 | N=$2^2$=4 | l=$\frac{1}{3}^2$=$\frac{1}{9}$ | L=$\frac{4}{9}$ |
| n=3 | N=$2^3$=8 | l=$\frac{1}{3}^3$=$\frac{1}{27}$ | L=$\frac{8}{27}$ |
$$L = exp[log(\frac{2}{3}^n] = exp[n\cdot(log(2) – log(3))] = exp[-\frac{log(l)}{log(3)} \cdot (log(2)-log(3))] = l^{1- (\frac{log(2)}{log(3)}})$$
$$L = l^{(1-D)}, \ D=\frac{log(2)}{log(3)}= 0.6309$$
La dimensione metrica dell’insieme triadico di Cantor è quindi frattale, non intera. Si dice essere più di un punto e meno di una linea.
Di strutture fini e autosimilarità
L’insieme frattale più noto a tutti è probabilmente il frattale di Mandelbrot che ho usato come immagine di copertina di questo articolo. Il nome dell’insieme è dovuto ad Adrien Douady, che lo nominò in onore del famoso pioniere polacco. Eccolo qui di seguito per poterlo osservare meglio.

Anche chi non mastica bene la matematica non può non rimanere affascinato da questa combinazione di forme e colori. Viene naturale analizzare la figura con intensità in cerca di quel pattern che si ripete, dei perimetri che delimitano le figure geometriche che tanto bene si conoscono. Tuttavia, come già capito, i frattali sono creature dalle proprietà meravigliose. Cercare di misurare il perimetro di questi oggetti è impossibile perché più si scende al dettaglio e si zoomma su un punto specifico, più la figura continua a frastagliarsi e a ripetersi ad ogni scala sempre più piccola e sempre più grande. E’ questo ciò che si intende per struttura fine, ed è questo che intendeva Mandelbrot quando proclamava l’impossibilità di misurare la costa inglese. Più si ingrandisce l’immagine più emergono dettagli che rivelano ulteriori forme e figure simili se non uguali a quelle di partenza.
Forse il fascino che emanano gli insiemi frattali sono percepiti dall’occhio umano che già sa, capisce che dovrà scandagliare a lungo l’oggetto del suo interesse in una rincorsa frenetica senza fine cui è destinato a fallire perché i frattali sono tutto fuorché statici. Sono oggetti impossibili che contengono l’infinito al loro interno.
Le proprietà uniche degli insiemi frattali, di struttura fine e di somiglianza a tutte le scale di osservazione, si formalizzano all’interno del concetto di auto-similarità. Dal punto di vista matematico, un insieme auto-simile è un compatto che può essere suddiviso in un numero finito di parti che sono copie omotetiche dell’insieme di partenza.
COSTRUIRE INSIEMI FRATTALI
La costruzione dei frattali si basa su un algoritmo di calcolo della velocità di convergenza di una funzione iterato un numero teoricamente infinito di volte. I modelli matematici che danno origine ai frattali presentano gradi diversi di complessità e solo recentemente, grazie all’avvento di computer sempre più potenti, si è riusciti ad entrare nei dettagli di queste fantastiche figure. Ad esempio, l’insieme di Mandelbrot si basa sulla formula della parabola traslata rispetto all’origine di un fattore c che ha come dominio il campo complesso: $$f(z) = z^2 + c$$ con $z=a+ib$ e $c\in \mathbb{C}$ fissato.
Formalmente, è l’insieme dei numeri complessi $c$ per i quali la successione $\{z_n\}_{n\in \mathbb{N}}$ definita da:
$$z_0=0$$
$$z_{n+1}=z_n^2 + c$$
è limitata, cioè per i quali esiste un $M$ tale che $\left| z_n \right| \leq M$, per ogni $n \in \mathbb{N}$.
La successione assume una forma del tipo:
$z_0=0$
$z_1=c$
$z_2=c^2+c$
$z_3=(c^2+c)^2+c$
…
Fissato un numero complesso c di partenza, l’insieme di Mandelbrot è costituito da soli quei punti in cui la successione converge e quindi la traiettoria si ritorce su se stessa. I punti di questo insieme vengono colorati di nero. I punti in cui la successione diverge, invece, vengono utilizzati usando colori diversi. Ogni colore starà ad indicare una diversa velocità di divergenza, ad esempio si potrebbe impiegare il rosso per i punti che divergono alla prima iterazione, l’arancione per quelli che divergono alla seconda e cosi via..
Gli insiemi di Julia
Gli insiemi di Julia rappresentano una famiglia di insiemi di numeri complessi $c$ per cui è limitata la successione:
$$z_0=c$$
$$z_{n+1}=z_n^2 + C$$
per un certo C fissato. Le differenze stanno: nel primo elemento della successione ($0$ per Mandelbrot e $z_0$ per Julia) e nell’addendo che nel caso di Julia non è il punto di cui si vuole verificare l’appartenenza, ma è un parametro fisso C. Gli insiemi di Julia possono essere connessi o non connessi. L’insieme dei numeri complessi C per i quali il relativo insieme di Julia è connesso è l’insieme di Mandelbrot.
Gli insiemi complementari a quelli di Julia sono gli insiemi di Fatou. I due matematici francesi Pierre Fatou e Gaston Julia, furono rivali lungo tutto l’arco della loro vita. Condividendo un campo di ricerca comune, la dinamica delle funzioni olomorfe, oggi vengono spesso, paradossalmente, citati insieme. Nel piano complesso, l’insieme di Julia sta ad indicare il luogo dei punti il cui comportamento dopo ripetute iterazioni della funzione è caotico: a seguito di una piccola perturbazione iniziale il comportamento della funzione cambia drasticamente. L’insieme di Fatou, invece, ne indica i luoghi di maggior stabilità.

Frattali geometrici e frattali stocastici
Come accennato poco sopra, esiste una classe di frattali non geometrici, i frattali stocastici, per la quale le proprietà degli insiemi frattali non vengono attribuite a forme geometriche bensì alle distribuzioni di probabilità che dominano moltissimi fenomeni fisici. Gli aspetti aleatori giocano, infatti, un ruolo molto importante nei fenomeni naturali e, quando sono coinvolti, è impossibile parlare semplicemente di frattali geometrici. I frattali stocastici rappresentano un campo d’indagine dalle infinite possibilità in quanto in grado di trattare fenomeni assai rilevanti per le attività umane: è il caso dell’andamento delle azioni di mercato, dello sviluppo di nuove antenne di dimensione contenuta, delle previsioni di piovosità, del diffondersi di una epidemia, persino coinvolgono l’arte di Pollock.
Non insisto ora in quest’articolo di per sé già lungo. Ho trattato l’esempio più semplice di frattale stocastico, il moto browniano frazionario, accessibile cliccando sul link associato, come espediente per trattare l’argomento.
Un libro che mi sento di consigliare sull’argomento é : Introduzione alla fisica dei frattali di Sergio Peppino Ratti. Un libro molto chiaro e comprensibile, che vanta la prefazione ad opera di Luciano Pietronero, il fisico che introdusse il concetto di cosmologia frattale.