Ti sei mai chiesto quali sono le tue reali possibilità di vincere al Superenalotto? O quali probabilità hai di avere una mano vincente a Poker? Rispondere a queste domande richiede una certa conoscenza di calcolo delle probabilità. In questo articolo ci approcciamo all’argomento, nel modo più intuitivo possibile. Alla fine proveremo a mettere in pratica quanto appreso con alcuni esercizi di calcolo delle probabilità. I manuali specialistici integreranno il resto. 🎲
In copertina, foto CC by 4.0 ad opera di Naser Tamimi su Unsplash
Definizioni preliminari
La teoria delle probabilità
La teoria delle probabilità è quella branca della matematica che si occupa di studiare e descrivere processi aleatori – da alea, in latino dado – ovvero processi dei quali non è possibile conoscere a priori il risultato finale, anche se si conoscono quelli che sono gli esiti possibili. Va da se che una componente fondamentale di questo studio è l’incertezza.
Per farlo sono stati imbastiti, nel corso dei secoli, un complesso di strutture, e definizioni che cercano ridurre il più possibile quel netto distacco fra l’imprevedibilità, per così dire, di certi eventi e una stima delle loro realizzazioni. Il tutto avviene mediante l’attribuzione di un numero – compreso fra 0 ed 1 – ad ogni evento casuale, che ne quantifichi la sua probabilità di realizzazione.
Lo scopo principale di tutta la teoria delle probabilità è quello di assegnare – in maniera coerente – un numero appartenente all’intervallo $[0, 1]$ ad uno più eventi di interesse. Questo numero prende il nome di probabilità.
Nel corso degli anni ti sarà capitato di incontrare varie definizioni del concetto di probabilità – dove con probabilità intendo implicitamente misura della probabilità -. Esiste la definizione classica, quella più antica, basata a priori su processi equiprobabili. Esiste la definizione frequentistica, basata sulla legge dei grandi numeri. Questa definizione avviene a posteriori, posto che tutti gli esiti possibili dell’esperimento si siano verificati (per questo se ne prende il limite all’infinito). C’è quella soggettiva bayesiana che include al suo interno un certo grado di fiducia e si rifà alle aspettative degli individui.
La probabilità assiomatica
A noi interessa la probabilità assiomatica, quella introdotta da Andrej N. Kolmogorov nel 1933 con soli tre assiomi, dalla quale discende la moderna teoria della probabilità.
Infatti, a prescindere dalla definizione che si vuole dare al concetto di probabilità, la teoria di Kolmogorov funziona comunque. I suoi tre assiomi non dimostrabili – sono, appunto, assiomi – vanno accettati e funzionano con tutte le definizioni che desideriamo usare.
La teoria della probabilità moderna che discende dagli assiomi introdotti da Kolmogorov nel 1933 vale sempre, qualunque sia la concezione probabilistica.
Gli assiomi di Kolmogorov
Gli assiomi introdotti da Kolmogorov rendono la probabilità assiomatica, quella più consistente sul piano matematico poiché si fonda su alcuni principi generali di teoria della misura. Vedremo ora che questi assiomi sono molto semplici e facili da ricordare. Sono però sufficienti a garantire una impalcatura solida allìapparato teorico che vi è stato costruito sopra.
Primo assioma di non negatività
La probabilità è un numero reale, maggiore o uguale a zero.
$$P(A)\geqslant 0$$
Secondo assioma di normalizzazione
La probabilità dell’evento certo è pari a 1.
$$P(\Omega) = 1$$
Terzo assioma di additività: finita e completa
Dati due eventi A e B incompatibili, tali cioè che $A\cap B=\emptyset$ si ha che
$$P(A \cup B)=P(A)+P(B)$$
Inoltre, data una famiglia composta da un’infinità numerabile di eventi $\{ A_i\}=\{ A_i; i=1,2,3,..\}$ a due due incompatibili, cioè tali che $A_i\cap A_j=\emptyset$ per ogni $i\neq j$, si ha che
$$P(\bigcup_{i=1}^{\infty}A_i)= \sum_{i=1}^{\infty}P(A_i)$$
Per capire meglio la novità introdotta da questa nuova visione dobbiamo prima fare un passo indietro e capire che cosa si intende per spazio probabilizzato. Una volta compreso saremo già in grado di risolvere i primi problemi di calcolo probatorio.
Definizioni centrali
Di insiemi e spazi campionari
La teoria delle probabilità si basa – tutta – sugli insiemi, che in linguaggio probabilistico vengono chiamati eventi, e sulle loro operazioni.
Gli insiemi sono collezioni di oggetti diversi non in ordine e che ammette operazioni di insieme quali: l’unione, la intersezione e il complementare.
Un evento – o insieme – $E$ va inteso come un risultato possibile, fra tutti i possibili esiti di un esperimento casuale. Per definizione, vive in uno spazio campionario $\Omega$.
Lo spazio campionario, o spazio campione, o spazio degli eventi $\Omega$ è l’insieme di tutti i possibili esiti di un esperimento aleatorio.
Quindi un evento $E$ è un sotto-insieme dello spazio campionario $E \in \Omega$. Un evento $E$ può essere:
- certo, se si è sicuri si avvererà $E=\Omega$
- impossibile, se non si avvererà mai $E=\emptyset$
- semplice, se coincide con un punto dello spazio campionario
- composto, se è dato da un insieme di eventi semplici, ovvero da un sotto-insieme $E\subseteq \Omega$
Due eventi distinti, A e B vengono detti disgiunti se
$$A\cap B=\emptyset$$
Inoltre, $\bar{A}$ è detto il complementare di $A$ se
$$A \cup \bar{A}=\Omega$$
Di insiemi misurabili e sigma algebra
Definiamo una $\sigma$-algebra come una famiglia $F$ di sotto-insiemi – o eventi – di $\Omega$ tale che:
- $\Omega\in F$ e anche $\emptyset \in F$
- $A$ è chiuso rispetto alla operazione di complemento : $$A \in F \Rightarrow \bar{A}\in F$$
- $A$ è chiuso rispetto alle operazioni di unione numerabile, ovvero, per ogni successione $A_i$ con $i=1,2,3..$ di insiemi appartenenti ad $F$ si ha che $$\bigcup_{i=1}^{\infty}A_i \in F$$ In questo caso abbiamo richiesto che l’unione sia numerabile e non finita per permettere il passaggio al limite.
La $\sigma$-algebra rappresenta la famiglia di tutto quegli eventi di cui ci interessa studiare il risultato. Quando alla famiglia di insiemi $F$ in $\Omega$ viene attribuita la struttura delle $\sigma$-algebra, allora, $\Omega$ viene chiamato spazio misurabile ed $F$ insiemi misurabili.
Una misura della probabilità
Arrivati a definire lo spazio campione e gli eventi che lo compongono, si rende necessario introdurre una funzione $P$ chiamata misura della probabilità, che è in grado di assegnare – in modo coerente – una variabile numerica a ciascuno degli eventi dello spazio campione.
La misura della probabilità, o più semplicemente probabilità, è una funzione $P$ che assegna ad ogni elemento di $F$ un numero compreso nell’intervallo fra 0 e 1.
Lo spazio delle probabilità ($\Omega$ ,$F$,$P$)
Finalmente, abbiamo tutto l’occorrente necessario per cucire su misura 💀 una teoria valida e potente in grado di fornire risposte precise a quesiti di natura esclusivamente randomica. Il tutto avviene per mezzo dello spazio di probabilità.
Lo spazio di probabilità è la terna $(\Omega,F,P)$. La terna è composta da uno spazio campionario $\Omega$, una famiglia di $\sigma$-algebra $F$ costruita su $\Omega$ e una funzione di probabilità $P$ definita sulle $\sigma$-algebra $F$.
Regole probabilistiche
Ci sembrerà strano. Anche se l’apparato probatorio e statistico che verrà costruito sopra la teoria assiomatica è notevole e complicato, già con le semplici regole introdotte finora, siamo in grado di formulare delle risposte valide ad esperimenti casuali. Facciamo un ultimo sforzo introducendo alcune operazioni d’insieme.
Eventi semplici o incompatibili
Definiamo due sotto-insiemi di eventi semplici – o elementari, o incompatibili – dello spazio campionario $\Omega$ come due suoi sotto-insiemi disgiunti. Chiamiamo questi sotto-insiemi A e B. Essi non hanno elementi in comune. I due evento si escludono a vicenda, e non possono verificarsi allo stesso momento. Si ha allora:
$$A\cap B=\emptyset$$

Eventi composti o compatibili
Al contrario, definiamo due eventi composti – o compatibili – dello spazio campionario $\Omega$ come due suoi sotto-insiemi non disgiunti. Chiamiamo questi sotto-insiemi A e B. Essi hanno degli elementi in comune e che appartengono al loro spazio di intersezione. Ciò significa che gli eventi che appartengono all’insieme intersezione di A e B possono verificarsi in contemporanea. Si ha:
$$A\cap B \neq \emptyset$$

La disgiunzione fa parte delle relazioni fondamentali della teoria degli insiemi. Le altre due sono la appartenenza e l’inclusione. Non dovrebbe essere difficile immaginare quelle che siano le loro proprietà. E’ comunque importante notare che la disgiunzione fra due insiemi non è transitiva.
Probabilità della somma logica di due eventi
(legge della somma)
Definiamo somma di due eventi il verificarsi dell’uno, dell’altro o di entrambi. La somma, nel linguaggio insiemistico, viene esplicitata dall‘operatore di unione. La probabilità di un evento C somma di due eventi A e B si esprime nel modo seguente: $P(C)=P(A \cup B)$. Distinguiamo fra due casi possibili:
- se gli eventi si escludono a vicenda – sono cioè eventi semplici o incompatibili – allora la probabilità che accada o uno o l’altro o entrambi è data da:
$$P(C)=P(A \cup B)=P(A) + P(B)$$ - se, invece, gli eventi non si escludono a vicenda – sono cioè eventi composti – allora la probabilità che accada o uno o l’altro o entrambi è data da:
$$P(C)=P(A \cup B)= P(A) + P(B) – P(A \cap B)$$
In questo caso infatti, se non sottraessimo la disgiunzione dei due andremmo a contarne il contributo due volte.
Probabilità del prodotto logico di due eventi
(legge del prodotto)
Definiamo prodotto di due eventi il verificarsi simultaneo di entrambi. Il prodotto, nel linguaggio insiemistico, viene esplicitato dall’operatore di intersezione. La probabilità di un evento C prodotto di due eventi A e B si esprime nel modo seguente: $P(C)=P(A \cup B)$. Anche in questo caso distinguiamo fra due casi possibili:
- se gli eventi sono mutuamente escludentesi – sono cioè eventi semplici o incompatibili- allora la probabilità che questi accadano insieme è nulla:
$$P(C)=P(A \cap B)=\emptyset$$ - se, invece, gli eventi non sono mutuamente escludentesi – sono cioè eventi composti o compatibili – allora la probabilità che questi accadano in simultanea non è nulla e vale:
$$P(C)=P(A \cap B) = P(A) + P(B) – P(A \cup B)$$
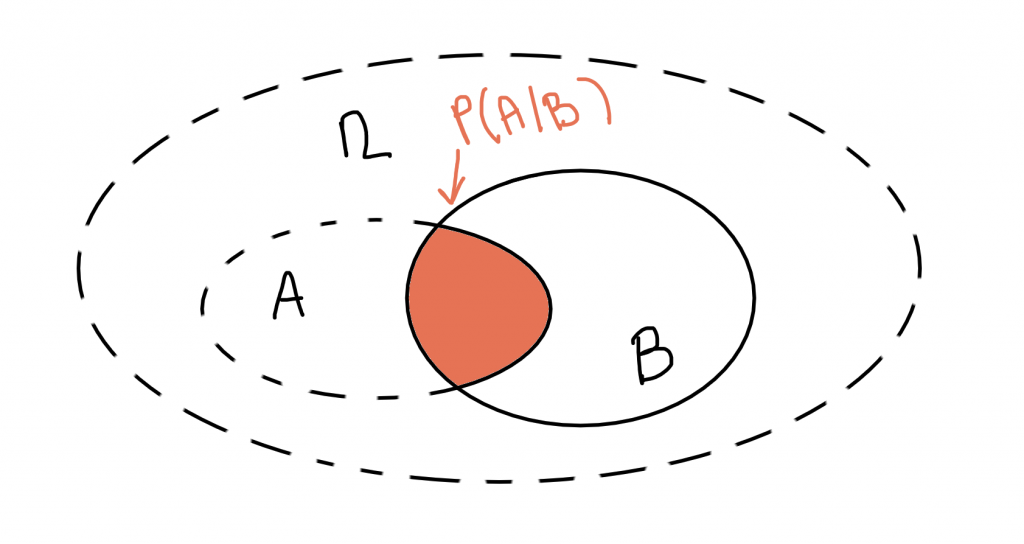
Probabilità condizionata
Se A e B sono due eventi dello spazio campionario $\Omega$, si definisce probabilità condizionale – o condizionata – di A dato B, e con ciò si intende la probabilità che si verifichi un evento di A dopo che si è verificato un evento di B, come:
$$P(A\mid B)=P(A\cap B)/P(B)$$
Da cui è possibile ricavare direttamente la formula per la probabilità composta come:
$$P(A\cap B)=P(A\mid B) \cdot P(B)$$
Problemi di calcolo delle probabilità
Siamo arrivati alla fine del post, sopravvivendo a definizioni su definizioni. Ciò significa che dovremmo essere in grado di risolvere i primi problemi. Proviamo con i seguenti.
I calzini spaiati
Sei di fretta, è notte e la lampadina della camera si è rotta. Devi prendere un paio di calzini dal cassetto del comò. I calzini sono spaiati e al tatto indistinguibili. Sai che nel cassetto ci sono 10 calzetti neri e 6 calzetti blu. Qual è la probabilità di averne presi due dello stesso colore?
Questo è un problema di probabilità condizionata. E’ inoltre un problema in cui tutti gli eventi sono equiprobabili. Per risolverlo facciamo un ragionamento a ritroso. Supponiamo di aver estratto un primo calzino. Chiamo la probabilità associata a questo evento P(N1) se il primo calzino è nero e P(B1) se il primo calzino è blu. Allora
- caso primo calzino nero
$$P(N1)=\frac{10}{16}=0.625$$
Cosa potrebbe succedere ora? Quali sono le possibilità di estrarne un secondo nero e quali blu?
Le uniche cose che cambiano rispetto alla prima stima sono la dimensione dello spazio campionario che da 16 calzini passa a 15 e il numero di eventi del sotto-insieme dei calzini neri che non sono più 10 ma 9. Chiamo la probabilità associata all’estrazione di un calzino nero P(N2) e chiamo la probabilità associata all’estrazione di un calzino blu P(B2)Allora:- La probabilità di estrarne un secondo nero è P(N2)=$\frac{9}{15}=0.6$
- La probabilità di estrarne un secondo blu è P(B2)= $\frac{6}{15}=0.4$
- caso primo calzino blu
$$P(B1)=\frac{6}{16}=0.375$$
Il ragionamento è analogo. La prima estrazione – cioè il primo evento A – ha ridotto la dimensione dello spazio campionario. E anche il numero degli eventi favorevoli si è modificato passando da 6 a 5. Ancora, chiamo la probabilità associata all’estrazione di un calzino nero P(N2) e chiamo la probabilità associata all’estrazione di un calzino blu P(B2). Allora:- La probabilità di estrarne un secondo nero è P(N2)=$\frac{10}{15}=0.667$
- La probabilità di estrarne un secondo blu è P(B2)= $\frac{5}{15}=0.333$
L’evento A estrazione di due calzini dello stesso colore corrisponde alla somma dei due eventi composti incompatibili che sono contenuti nelle due parentesi tonde:
$$A=(N1 \cap N2) \cup (B1 \cap B2)$$
Nel nostro problema gli eventi sono dipendenti fra loro. L’estrazione del primo calzino si ripercuote sulla seconda estrazione. Di conseguenza, la probabilità totale di averne appaiati è data da:
$$P(A)=P(N1 \cap N2)+P(B1 \cap B2)= P(N1) \times P(N2 \mid N1) +P(B1) \times P(B2 \mid B1)$$
Dove abbiamo appena usato la legge delle probabilità composte per eventi dipendenti. Quindi:
$$P(A)= 0.625 \cdot 0.6 + 0.375 \cdot 0.333 =0.375+0.125=0.5$$
I re nel mazzo
Hai in mano un mazzo di 52 carte, ben mescolato. Chiedi a un tuo amico di estrarne 2 a caso, senza vederne le figure. Qual è la probabilità di estrarre 2 re?
In questo problema occorre innanzitutto sapere che i re nel mazzo sono 4. Anche in questo caso gli eventi sono dipendenti e si usano le formule di calcolo condizionale. A questo punto possiamo procedere andando a definire la probabilità che si verifichi il primo evento favorevole, la prima pescata di un re. Chiamiamo questo evento A.
$$P(A)=\frac{4}{52}$$
Andiamo a definire la probabilità che si verifichi il secondo evento favorevole, la seconda pescata di un re. Chiamiamo questo evento B.
$$P(B\mid A)=\frac{3}{51}$$
Sappiamo che $$P(A\cap B)=P(B\mid A) \cdot P(A)=$$
$$=\frac{3}{51} \cdot \frac{4}{52}=\frac{12}{2652}=0.00452$$
La probabilità di estrarre due re consecutivi è poco più di uno su mille.
Come cambierebbe il problema se volessi calcolare la stessa probabilità ma reinserendo la prima carta estratta, rimescolando e solo in seguito estraendo la seconda?
In questo caso il problema non è più condizionato, è chiaro. Resta da stabilire se questo comporta una maggiore o minore possibilità di pescare la carta giusta. In questo caso sappiamo che:
$$P(A)=P(B)=\frac{4}{52}$$ visto che reinserisco la prima carta nel mazzo dopo averla estratta. Allora:
$$P(A\cap B)=P(A) \cdot P(B)=\frac{4}{52} \cdot \frac{4}{52} =0.00592$$
Come ci si sarebbe aspettato, abbiamo più possibilità di pescare una seconda volta il re se reinseriamo il primo all’interno del mazzo.
Obesità e diabete
Hai appena letto un articolo in cui viene riportato che il 30% degli adulti negli Stati Uniti sono obesi, che il 3% sono diabetici e che il 2% sono sia obesi che diabetici. Vuoi determinare la probabilità che un individuo scelto casualmente fra la popolazione sia diabetico se è obeso e sia obeso se è diabetico.
Ormai dovremmo essere in grado di risolvere questi problemi. In questo caso abbiamo già tutte le informazioni che ci servono, occorre solo inserirle nelle formule corrette.
- Sia P(A) la probabilità che un individuo americano sia obeso. P(A)=0.3
- Sia P(B) la probabilità che un individuo americano sia diabetico. P(B)=0.03
- Sia $P(A \cap B)$ la probabilità che un individuo americano sia obeso e diabetico. $P(A \cap B)=0.02$
Allora $$P(B \mid A)= P(B \cap A) /P(A)= \frac{0.02}{0.3}=0.067$$
$$P( A\mid B)= P(B \cap A) /P(B)= \frac{0.02}{0.03}=0.667$$
Questi problemi sarebbero stati più immediati da risolvere se avessimo introdotto il calcolo binomiale di Newton. Ci riserviamo di farlo in un nuovo post. Alla prossima!