Nonché l’analisi di un esempio su tutti: la deposizione balistica e l’equazione di Khadar Parisi e Zhang.

Seppur argomenti chiave in grado di fornire una base teorica al comportamento dei sistemi fisici prossimi ai punti critici (nelle transizioni di fase critiche) di dominio della meccanica statistica, in cui sono stati inizialmente studiati ed introdotti, sappiamo molto bene che in natura le scienze sono indispensabili tutte nella descrizione completa di qualsiasi fenomeno e, soprattutto in fisica, l’interdisciplinarietà è inevitabile. In questo articolo voglio introdurre i concetti ripresi nel titolo in funzione della loro comparsa all’interno dei modelli di crescita superficiale già studiati qui e qui. Gli esponenti critici (o coefficienti di scala) che vedremo sono 3, nonostante ne esistano molti altri che servono a descrivere la transizione fra i diversi stati cui può trovarsi la materia: stati di aggregazione delle molecole (solido, liquido, vapore), stati di magnetizzazione (paramagnetismo, diamagnetismo, ferromagnetismo), stati di conduzione (fluido, superfluido). Per ora, quelli che ci interessano sono:

• $\alpha$ coefficiente di roughness
• $\beta$ coefficiente di crescita
• $z$ coefficiente dinamico

Se sono ben noti i processi di deposizione di film sopra citati, non ci si deve stupire del fatto che tutti e tre gli esponenti critici siano in grado di descrivere perfettamente l’evoluzione temporale della ampiezza di interfaccia all’interno di un range temporale ben preciso. In effetti, gli esponenti critici sono strumenti introdotti per approssimare le funzioni di stato laddove esse evolvono come potenze, e dove non seguono più le leggi fisiche valide per qualsiasi altri valori del dominio.  Essi intervengono in quelli che sono noti come punti critici del sistema. In un processo di deposizione superficiale, l’ampiezza di interfaccia del sistema – ben lontano dall’essere in una condizione di equilibrio – manifesta un andamento variabile nel tempo che è ben approssimato da leggi di potenza che hanno per esponenti i coefficienti $\alpha$, $\beta$ e $z$.

Andando ad approssimare il comportamento di una funzione di stato nei pressi di alcuni punti del tutto particolari, qualora si dovessero trovare funzioni caratterizzate dagli stessi valori dei coefficienti di scala, queste verrebbero considerate far parte della stessa classe di universalità: andrebbero a descrivere cioè fenomeni formalmente diversi ma che sono descritti dalle stesse leggi evolutive.

Il nome  di esponenti critici è dovuto al fatto che sono stati introdotti proprio per approssimare le funzioni di stato con delle leggi di potenza nei pressi dei punti critici, punto in cui la funzione energia presenta una discontinuità di secondo ordine. Talvolta vengono anche indicati come esponenti di scala e l’associazione qui si fa meno intuitiva. In realtà, se prendiamo come riferimento la potenza di una funzione qualsiasi ci possiamo accorgere che, qualora la scala del sistema di riferimento cambi di dimensione, la potenza della funzione varia con essa ed è a tutti gli effetti un’invariante di scala.

Ora per ritornare ai processi di deposizione già affrontati, se andiamo a confrontare, ad esempio, gli esponenti di scala della deposizione balistica ottenibili per via numerica, con gli esponenti di scala della equazione KPZ l’intelletto ci suggerisce che i due facciano parte  della stessa classe di universalità poiché i valori ottenuti sono molto simili tra loro. Nel caso più semplice 1+1 dimensionale (1 dimensione spaziale e 1 temporale) si hanno i seguenti:

• $\alpha$ = $\frac{1}{2}$
• $\beta$ = $\frac{1}{3}$
• $z$ = $\frac{3}{2}$

Aumentare la dimensione del sistema è possibile ma porta a meno predizioni. Per ora mi accontento di seguire l’evoluzione di una curva nello spazio-tempo. Nella deposizione random, il processo di crescita di ogni colonna è un processo di Poisson indipendente, non vi è correlazione e l’altezza di ogni colonna evolve come t^1/2. Anche il processo di crescita della deposizione balistica è di colonna in colonna indipendente; tuttavia, qui, un mattoncino si attacca al primo altro mattoncino che trova. Quindi se cade lungo una colonna posta in x ma la altezza della colonna in x+1 o x-1 è più alta di quella selezionata allora il mattoncino si attacca all’ultimo elemento della colonna vicina più alta. L’altezza delle colonne non è più indipendente e il sistema presenta correlazione spaziale.

REGIME DI POISSON – CRESCITA LINEARE

In realtà, esiste un tempo che parte da una condizione di superficie liscia senza alcuna deposizione e dura fino a che il processo rientra nel regime in cui domina il rumore shot (dall’inglese shot-noise) o rumore Schottky, fino a quando cioè il processo può essere catalogato come di Poisson – questo vale per i primi layer di materiale depositato- in cui il sistema non ha correlazione.

REGIME DI SATURAZIONE – ANDAMENTO COSTANTE

Superati i primi layer, l’interfaccia di superficie del sistema in accrescimento che, ora, presenta correlazione, aumenta di ampiezza fino ad un punto limite oltre il quale essa rimane costante per qualsiasi istante temporale futuro e si dice aver raggiunto il regime di saturazione.Il tutto è molto intuitivo. Nelle deposizioni balistiche, lo “sticking” laterale che si propaga di step in step fa si che l’informazione si propaghi lateralmente e il sistema divenga in qualche modo conscio di tutte le sue parti in contatto. Solo quando la lunghezza di correlazione (una funzione fondamentale per questo genere di indagini) eguaglia la lunghezza del sistema e quindi l’informazione viene passata anche fra gli elementi agli estremi del sistema, esso raggiunge il regime di saturazione.

REGIME INTERMEDIO – LEGGE DI POTENZA

Tra i due comportamenti estremi troviamo un andamento per la ampiezza di superficie che segue una legge di potenza. Dovrebbe essere ben chiaro che leggi di potenza e invarianza di scala vanno a braccetto. Le funzioni di potenza sono, per definizione, scalabili, ovvero auto-simili al variare della scala di osservazione e si manifestano ogni volta che in un fenomeno prevalgono le interazioni non lineari e le cause non sono proporzionali agli effetti.

GRAFICO BILOGARITMICO DELLA EVOLUZIONE DELLA AMPIEZZA DI INTERFACCIA

Per meglio riassumere questi concetti, proviamo ad analizzare il grafico seguente ricordando che:

1. 1. La morfologia di una superficie, e quindi la sua roughness, è descritta dalla ampiezza di interfaccia $w(L,t)$ definita come la deviazione standard dell’altezza media. Data $h(i,t)$ altezza di un singolo sito e $\bar{h(t)}=\frac{1}{L}\cdot\sum_{i=1}^{L} h(i,t)$ altezza media spaziale di una realizzazione del sistema, l’ampiezza di interfaccia si esprime facendo una media sull’ensemble, cioè sulle possibili realizzazioni del sistema $$w(L,t)=\sqrt{\frac{1}{L}\cdot\sum_{i=1}^{L}[h(i,t)-\bar{h(t)}]^{2}}$$  laddove in alcuni testi viene eliso il fattore di normalizzazione del sistema $\frac{1}{L}$ per far sì che durante la crescita iniziale per valori di $t\ll t_x$ l’ampiezza di interfaccia sia indipendente dalla dimensione del sistema
   2. La funzione di correlazione laterale $x(t)$ è quella funzione che dipende dalla funzione di correlazione delle altezze $C(x,t)$ che viene impiegata per giustificare il regime di saturazione dei sistemi che presentano correlazione
   3. Per un gran numero di modelli di crescita, compreso il caso in esame, è comunemente accettata la relazione di scaling di Family – Vicsek $$w(L,t)\sim L^{\alpha}\cdot f(\frac{t}{L^z})$$ in cui la funzione di scaling $f(x)$ è costante per valori molto grandi di x e va come $x^\beta$ per valori molto piccoli di x.
   4. $\alpha$, $\beta$ e $z$ non sono tra loro indipendenti ma sono legati dalla relazione $z=\frac{\alpha}{\beta}$

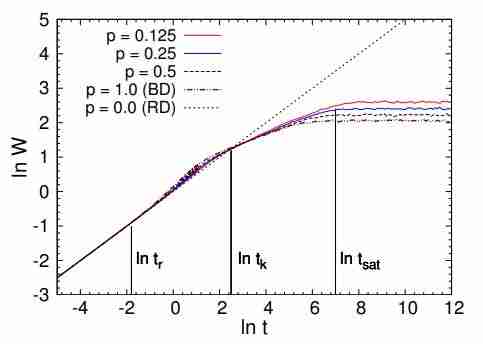
Il grafico ripreso dal paper “Surface properties and scaling behavior of a generalized ballistic deposition model in (1 + 1)-dimension” di Baisakhi Mal, Subhankar Ray e  J. Shamanna mostra tre diversi crossover-time t_r, t_k e t_sat che discriminano tra 4 diverse regioni in cui l’andamento dominante segue leggi di crescita diverse:

• Nella prima regione che dura per pochi monolayers, l’andamento dominante è quello di una deposizione random senza alcuna correlazione. Infatti, la lunghezza di correlazione laterale ivi è talmente piccola da poter considerare la crescita di ogni singola colonna come completamente indipendente dalle altre
• Nella seconda regione il comportamento predominante è quello di una legge di potenza caratterizzata dal coefficiente beta di scaling noto come esponente di crescita. Il fatto che in questa regione l’ampiezza di interfaccia, che è una grandezza globale, segua l’andamento di una potenza fa intuire la possibilità che il processo in gioco, autoaffine, sia a tutto gli effetti un frattale stocastico
• Nella terza regione, quella di transizione fra la crescita e la costanza della ampiezza di interfaccia è caratterizzato dal coefficiente di scaling zeta noto come esponente dinamico.
• Nella quarta regione, quella di saturazione, la ampiezza di interfaccia cessa di crescere. Essa è caratterizzata dall’esponente di roughness alfa, il coefficiente critico che, se noto, fornisce importanti informazioni sulla morfologia della superficie.

SCALING DINAMICO

È interessante valutare il legame presente fra la morfologia di superficie e le grandezze:

• $w(L,t)$ ampiezza media di superficie
• $C(L,t)$ funzione di correlazione delle altezze

Parlare di morfologia o di roughness di una superficie è la stessa cosa. Se la superficie non è perfettamente liscia (cioè non siamo nel caso ideale) allora è per forza più o meno rugosa. Il livello di roughness si può misurare statisticamente attraverso il coefficiente $\alpha$ (coefficiente di roughness) con il quale si intende, in senso globale, la funzione $w(L,t)$ o, in senso locale, la funzione $c(L,t)$. In quest’ultimo caso, $\alpha$ viene spesso indicato come indice di Hurst. $w(L,t)$ rappresenta di per sé una proprietà globale. Basti pensare a come viene presa la media per convincersene. Per ogni punto del dominio viene presa l’altezza della colonna corrispondente e ne viene fatta la media sul sistema stesso e su un ensemble di sue realizzazioni. Viceversa $c(L,t)$ rappresenta una proprietà locale. Si ottiene facendo la media di insieme di due punti diversi qualsiasi del dominio e ovviamente ciò non può definire una grandezza globale.

Le due grandezze non sono equivalenti poiché scalano diversamente al variare delle dimensioni del sistema. Tuttavia, quando il rumore è non correlato (rumore bianco) esse possono essere identificate in una grandezza sola. E’ il caso della deposizione balistica. Quando, invece non è così e il rumore è correlato (rumore reale) le due grandezze assumono valori diversi, scalano diversamente e, infatti, si parla di scaling anomalo. Rimanendo concentrati sui risultati ottenuti per la deposizione balistica, ecco come ottenere il corretto rescaling della ampiezza di scala visualizzato poco sopra.

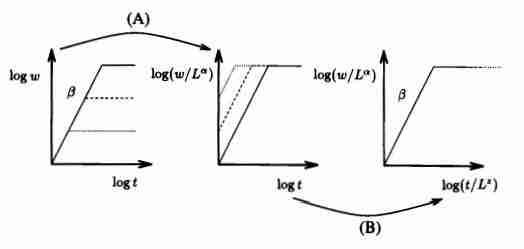
Il punto di partenza è il piano bilogaritmico che esprime la dipendenza di $w(L,t)$ da $t$ mentre il punto di arrivo è la relazione di scaling di Famiy-Vicsek. Si procede nel modo seguente:

1. Per prima cosa occorre riscalare la ascissa $w(L,t) \rightarrow \frac{w(L,t)}{w(t)}$ così che le ampiezze di superficie graficate per diversi $L$ saturino allo stesso valore (processo A)
2. In secondo luogo occorre riscalare l’ordinata in funzione del tempo di crossover $t \rightarrow \frac{t}{t_x}$ cosi da far in modo che, indipendentemente dalla taglia del sistema e dal tempo di crossover, le ampiezze saturino anche per lo stesso valore della variabile indipendente.

Nelle considerazioni espresse c’è tutto ciò che è necessario per trovare la relazione esistente tra gli esponenti di scala.