Analizzeremo più al dettaglio, ma sempre in modo intuitivo, il moto browniano frazionario inteso come prototipo esemplare fra processi stocastici correlati. Prima di affrontare questo articolo, è vivamente consigliato aver dato prima un’occhiata al precedente e introduttivo: “Il moto browniano frazionario e l’indice di Hurst“. Mai – mai – entrare nei dungeons senza armi e armature adeguate 🗡️
In copertina, photo by Dylan Calluy on Unsplash CC by 4.0
Possiamo definire il moto browniano frazionario, da qui in poi fBm, a partire dal concetto di distribuzione normale – o gaussiana -. Il fBm descrive un processo stocastico che può essere sia discreto che continuo. A seconda del particolare fenomeno analizzato, è possibile considerare il tempo come variabile indipendente rispetto alla quale la funzione aleatoria si manifesta in una sua realizzazione.
Il moto browniano frazionario
Definizione
Il moto browniano frazionario è un processo gaussiano centrato $B^H=\{B^H_t\}_{t \geq 0}$ con funzione di covarianza
$$\mathbb{E}(B_t^H,B_s^H)=\frac{1}{2} (\left | t \right |^{2H}+\left | s \right |^{2H}-\left | t-s \right |^{2H})$$
Il processo è caratterizzato da un parametro $H$ detto indice di Hurst che può assumere solo valori compresi fra 0 ed 1.
Essendo caratterizzato da un comportamento gaussiano, che è ben identificato qualora ne siano ben definiti media e covarianza, andremo ora ad approfondire il significato delle due per poi passare a vedere le peculiarità che il moto presenta a seconda del valore assunto dal parametro $H$.
Tre sono le proprietà che caratterizzano il fBm e che ne definiscono la statistica:
- $X_0=0$ quasi certamente, cioè $P(X_0=0)=1$
- per ogni $t>0$ $$X_t\sim N(0,\sigma^2 \left | t \right |^{2H})$$ con $N$ distribuzione normale
- se valori di $H=\frac{1}{2}$ allora $B^{\frac{1}{2}}$ si riduce al moto browniano
A tal proposito, avremmo potuto definire fin da subito il fBm attraverso concetti di spazio probabilistico e sigma-algebre, nel modo seguente:
Il moto browniano frazionario è un processo stocastico normale $B^H=\{B^H_t\}_{t \in I}$, H-sssi adattato alla filtrazione.
Per capire cosa si intende con processi H-sssi e filtrazioni rimando al fondo pagina. Puoi arrivarci direttamente cliccando qui.
Caratterizzazione del moto browniano frazionario
- Un processo descritto da una distribuzione normale è un processo simmetrico. Il punto a cui corrisponde la media, cioè il valore che capita più di frequente – e che potrebbe non essere una realizzazione del sistema – coincide con il punto di simmetria della distribuzione.
L’essere a incrementi stazionari, unito alla condizione quasi certa che $X_0=0$ fa si che il processo sia a media nulla, inoltre $X(-t)=-X(t)$
Quando si ha a che fare con processi stocastici, si è soliti introdurre una funzione $f(x): \mathbb{R} \rightarrow \mathbb{R}$ chiamata densità di probabilità con le proprietà che:
$$f(x) \geq 0$$
$${\int_{-\infty}^{+\infty} f(x) }dx = 1$$
A variabili aleatorie continue è sempre possibile associare una densità di probabilità $f(x)$. Allora la probabilità di un evento A viene calcolata come:
$$P(x \in A)={\int_{A} f(x) }dx$$
In questo senso, con media – o valore atteso – $\mathbb{E}[X(t)]$ intendiamo la media dei valori pesati con le loro probabilità, o la somma dei valori per le loro probabilità.
$$\mu(t)= \mathbb{E}[X(t)] ={\int_{-\infty}^{+\infty} x f(x) }dx$$
- Il fatto di essere un processo ad incrementi stazionari, unito alla condizione quasi certa che $X_0=0$ e alla proprietà che $\sigma^2=\mathbb{E}(X_1^H)$, fa si che valga:
$$\mathbb{E}(X_t^H)=\left | t \right |^{2H} \sigma^2$$
Con varianza – o scarto quadratico medio– $\mathbb{E}[(X(t)-\mu(t))^2]$ intendiamo il momento secondo rispetto alla media – che nel nostro caso è nulla -. Con ciò vogliamo quantificare la dispersione della funzione di densità della variabile aleatoria rispetto alla media e scriviamo:
$$\sigma^2= \mathbb{E}[(X(t)-\mu(t))^2]=\mathbb{E}[(X(t)]^2= {\int x^2 f(x) }dx$$
La definizione di varianza ci permette di introdurre, in modo analogo, quella di covarianza
$$Cov[X]=Var(X,X)$$
In generale, quindi:
$$Cov(X,Y)= \mathbb{E}[(X-\mu_X)(Y-\mu_Y)]$$
$$=\int_{X=-\infty}^{+\infty} \int_{Y=-\infty}^{+\infty}XYf(X,Y)dYdX$$
Attraverso la covarianza è possibile introdurre il coefficiente di correlazione che lega le variabili dipendenti X e Y.
$$\rho(X,Y)=\frac{Cov(X,Y)}{\sqrt{Var[X]Var[Y]}}$$
In caso contrario, se le variabili fossero indipendenti avremmo avuto $\rho(X,Y)=0$.
- La covarianza del moto browniano frazionario, spesso indicata come $\Gamma^H_{s,t}$, è caratterizzata dalla seguente espressione:
$$\mathbb{E}(B_t^H,B_s^H)=\frac{1}{2} (\left | t \right |^{2H}+\left | s \right |^{2H}-\left | t-s \right |^{2H})$$
Il caso $H=\frac{1}{2}$ si riduce al moto browniano. Infatti, la $\Gamma^H_{s,t}$ diventa:
$$\Gamma_{s,t}=\left\{\begin{matrix}
min (\left | s \right |,\left | t \right |) & se \frac{\left | s \right |}{s}=\frac{\left | t \right |}{t}\\
0 & altrimenti
\end{matrix}\right.$$
Plot di evoluzione di un processo browniano frazionario
Nel grafico che segue, dovremmo già essere in grado, per quanto visto finora, di associare a ciascun processo illustrato, il corretto range dell’indice di Hurst. Ricordiamoci che l’intervallo di interesse per avere un effetto Hurst si ha per valori compresi fra 0 ed 1. Per valori di H superiori, infatti, l’autocorrelazione crescerebbe troppo per avere significato mentre per valori di H negativi la autocorrelazione positiva decade troppo rapidamente. Andiamo a studiare, dunque, quel che accade all’interno di due distinti range:
- Per valori dell’indice di Hurst $H=\frac{1}{2}$ il fenomeno che stiamo osservando è un processo di moto browniano, puramente caotico. L’indice di auto-covarianza è nullo $\Gamma_t^H=0$. Il corrispondente rumore $h=h_t$ è il rumore bianco chiamato anche white noise
- Nel caso in cui l’indice di Hurst dovesse assumere valori compresi nell’intervallo $\frac{1}{2}<H<1$ la serie sarebbe persistente. Il processo avrebbe auto-covarianza positiva $\Gamma_t^H>0$ e la somma corrispondente divergerebbe $\sum_{t=1}^{\infty}\Gamma_t^H$. Il corrispondente rumore $h=h_t$ sarebbe chiamato black noise
- Infine, per valori dell’indice di Hurst compresi nell’intervallo $0<H<\frac{1}{2}$ la serie sarebbe anti-persistente, con indice di auto-covarianza negativo $\Gamma_t^H<0$ e la somma corrispondente convergerebbe $\sum_{t=1}^{\infty}\Gamma_t^H$. Il corrispondente rumore $h=h_t$ sarebbe chiamato pink noise
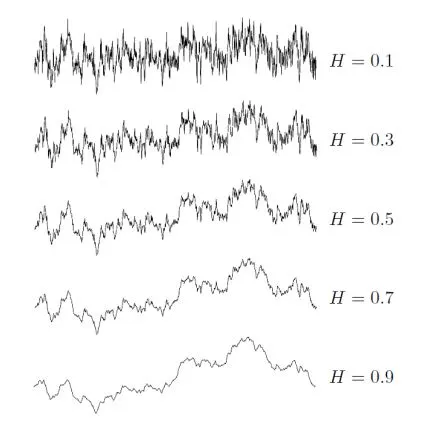
Vale la pena notare che, diversamente dal moto browniano, il moto browniano frazionario non è né un processo di Markov né una martingala.
Un libro completo, specifico dell’argomento che mi sento di consigliare a chi di queste cose ne fa mestiere è il “Selected Aspects of Fractional Brownian Motion” che si può trovare nelle biblioteche universitarie.
Rumore gaussiano frazionario
La consistenza dell’approssimazione dei mercati finanziari attraverso un modello browniano frazionario è tangibile quando quest’ultimo viene applicato per la creazione di sequenze gaussiane stazionarie – che mettono in evidenza correlazioni di lungo periodo – e sequenze con intermittenza – per fenomeni turbolenti -. Consideriamo il seguente processo incremento:
$$h(t)=B_t^H – B_{t-1}^H, \ \ \ \ \ \ t \geq 1$$
la sequenza $h=h(t)_{t \geq 1}$ è il rumore gaussiano frazionario ed è legato all’indice di Hurst $H$. In particolare:
- se $0<H<\frac{1}{2}$ la sequenza non presenta dipendenza da lunga portata
- se$\frac{1}{2}<H<1$ presenta dipendenza di lunga portata
Processi stocastici a tempi continui
Diamo per scontato di sapere come è definito uno spazio di probabilità. In caso contrario l’articolo: “Che cosa si intende per probabilità?” potrebbe esserci di aiuto. Se siamo in grado di definire uno spazio probabilistico, siamo anche in grado di definire in processo stocastico a valori reali.
Sia $(\Omega, F,P)$ uno spazio di probabilità e sia $I \in [0,\infty)$ un intervallo che va da zero a infinito.
Un processo stocastico a valori reali è una famiglia $\{X_t\}_{t \geq 0}$ di variabili aleatorie reali definite sullo spazio di probabilità tali che: $$X_t: \Omega \rightarrow \mathbb{R}^N, \ \ \ \ \ \ {t \in I}$$
Va da se che i processi stocastici costituiscono uno strumento per rappresentare in modo probabilistico
quantità incerte che evolvono nel tempo. Nella realtà questo avviene per tempi continui, e il processo viene definito processo stocastico a tempi continui. Con ciò si intende che l’insieme dei tempi coincide con l’insieme dei numeri reali.
Un processo stocastico a tempo continuo è qualsiasi famiglia $\{X_t\}_{t\geq 0}$ di variabili aleatorie indicizzata dal tempo $t \in [0,\infty)$.
Pensiamo di effettuare un qualche tipo di esperimento: la rilevazione delle temperature o delle velocità dei venti di una località, la misura delle altezze di piene dei fiumi ecc… Chiamo i possibili risultati di questo esperimento realizzazioni. Le realizzazioni del processo stocastico – o serie storiche – sono funzioni aleatorie del tempo, che sono state scelte casualmente fra tutte le altre funzioni possibili.
Le serie storiche sono importanti perché permettono di fare inferenza sul modello.
Caratterizzazione del processo stocastico
Un processo stocastico $X=\{X_t\}_{t \in I}$ è detto processo ad incrementi stazionari – si indica con si – se per ogni $h \geq 0$ con $h \in \mathbb{R}$ vale:
$$\{ X_{t+h}-X_{h}\}_{t \geq 0}=\{X_t-X_0\}_{t \geq0}$$
Cioè, la stazionarietà degli incrementi richiede solo che la legge al tempo t dipenda dalla differenza fra le variabili temporali e non da t solamente. Ciò non implica una stazionarietà del processo stesso $\{X_t\}_{t \in I}$. Viceversa, un processo stazionario – un processo in cui le distribuzioni non variano – implicherebbe, invece, una stazionarietà anche degli incrementi
Un processo stocastico $X=\{X_t\}_{t \in I}$ è detto auto-similare – si indica H-ss – se un cambiamento di scala dei tempi $t \rightarrow at$ ha gli stessi effetti di un cambiamento di scala dello spazio $x \rightarrow xb$. Il processo manifesta quindi una invarianza di scala: esso cioè rimane invariante rispetto alla scala utilizzata per descrivere il fenomeno. Per ogni a>0 esiste un b>0 tale che $$\{X_{at}\}_{t \geq 0}=\{bX_t\}_{t \geq 0}$$ se $b=a^H$ allora $H$ è l’indice di Hurst.
Possiamo caratterizzare, ulteriormente, un processo stocastico come processo Hssi, se è un processo auto-similare a incrementi stazionari e con indice di Hurst $H$.
Oppure possiamo definirlo processo H-sssi se è un processo auto-similare, a incrementi stazionari e con indice di Hurst $H<1$.
E’ molto importante, infine, introdurre il concetto di filtrazione poiché: un processo stocastico $X$ adattato alla filtrazione $F_t$ è $F_t$-misurabile per ogni t.
Sia $F_t=\{F_t\}_{t \in I}$ una famiglia crescente di sotto $\sigma$-algebre di $F$ che contengono l’evento di misura. Allora $F_t$ è detta filtrazione.
Intuitivamente, la filtrazione rappresenta tutta l’informazione disponibile fino al tempo $t$. Ci dice cioè quali eventi si siano verificati e quali non.