Questo è l’articolo conclusivo di tutto il percorso che ha avuto come fulcro il metodo di approssimazione degli elementi finiti (da qui in poi FEM): un metodo numerico di risoluzione di problemi differenziali, siano essi alle derivate parziali o totali. Per recuperare gli articoli precedenti è sufficiente cliccare i seguenti link:
- articolo 1 – introduzione ed equazione delle onde
- articolo 2 – formulazione debole e principio dei lavori virtuali
- articolo 3 – il metodo Galerkin
Gli articoli sono stati ampliati attraverso l’uso di due teoremi:
Come spesso accade, forse si è in grado di comprendere appieno la potenza del metodo FEM solo attraverso un esempio pratico, per cui rimando al fondamentale:
Come per altri metodi, lo scopo del FEM è quello di ricondurre un sistema di equazioni differenziali ad un sistema di equazioni algebriche risolvibili dal calcolatore. Resta solo un piccolo ultimo sforzo e tutta la metodologia arriverà presto alla conclusione. Preparato il caffè? Bene. Andiamo avanti. Per poter applicare il metodo FEM è necessario che siano garantiti i seguenti requisiti:
- l’esistenza di una triangolazione del dominio
- la costruzione di un sottospazio di dimensione finita costituito da polinomiali a pezzi
- l’esistenza di funzioni di base avente supporto limitato
Fatto ciò sarà possibile implementarlo in codici numerici per la risoluzione di molteplici problemi della fisica. Io non ne darò una definizione rigorosa, per questo rimando a dei testo specifici di autori autorevoli (nome del libro e autore). Quel che voglio fare è passarne l’idea. Partiamo da alcune semplici definizioni:
TRIANGOLAZIONE DEL DOMINIO
La triangolazione è la partizione di una superficie compatta $S$ (ad esempio una sfera o un disco chiuso comprendente il bordo) data da una famiglia finita di sottospazi chiusi $\left \{ T_1,T_2,…,T_N \right \}$ che ricoprono la superficie, e da una famiglia finita di omeomorfismi tali che, per ogni $i,j=1,…,N$ con $i\neq j$ solo una delle seguenti condizioni sia soddisfatta da due sottospazi:
- $T_i$ e $T_j$ sono disgiunti
- $T_i$ e $T_j$ hanno in comune un solo vertice
- $T_i$ e $T_j$ hanno in comune due vertici e il lato che li connette
Ad esempio, una possibile e semplice triangolazione della superficie terrestre prevede di dividere la sfera in delle sezioni triangolari: il triangolo rappresenta in questo caso il sottospazio chiuso con cui si ricopre la superficie, mentre l’omeomorfismo è dato dalla deformazione che rende più convesso il triangolo nonché dalla rotazione dello stesso.
Una triangolazione è il punto di partenza fondamentale per poter approssimare il dominio di interesse e deve essere possibile per potervi applicare il metodo degli elementi finiti. Questo punto di primaria importanza, spesso non viene citato poiché, di fatto, ogni superficie topologica compatta è triangolabile.
SOTTOSPAZIO FINITODIMENSIONALE DI POLINOMI A PEZZI
Come secondo step occorre definire uno spazio di dimensione finita $X_{h}$ adatto ad approssimare lo spazio di dimensione infinita $X$. Come già accennato (qui) la scelta ricade su spazi formati da polinomi continui a tratti definiti su suddivisioni del dominio chiamate triangolazioni. I sottodomini in cui è partizionato il dominio di definizione vengono chiamati “elementi finiti”. Ogni elemento finito ha dimensioni molto più piccole della più piccola lunghezza caratteristica con cui varia significativamente la soluzione. Attraverso una scelta opportuna della forma e del numero di elementi finiti è possibile partizionare adeguatamente domini di forma complessa.
Chiamo $P_k$, con $k\geqslant0$ lo spazio dei polinomi di grado minoro o uguale a k nelle variabili $x_1,…,x_d$ e $X_h$ lo spazio degli elementi finito triangolari cioé
$X_h=X_h^k:=\left \{ v_h\in C^0(\Omega)\mid v_{h\mid k}\in P_k \forall k\in T_h \right \}, k\geqslant1$
Per descrivere le polinomiali a pezzi si usano i gradi di libertà che in questo caso sono i nodi dei sottoinsiemi $T_N$.
Il “supporto” di una funzione è la parte del suo dominio di definizione dove è diversa da zero.
FUNZIONI BASE
Le funzioni di base dello spazio $X_h$, spesso indicate come shape functions (funzioni di forma) sono in numero uguale al numero dei nodi (punti nodali, punti in cui avviene la suddivisione tra i vari elementi finiti) che determinano la struttura geometrica della partizione adoperata e che, per questo motivo, vengono anche chiamati gradi di libertà.
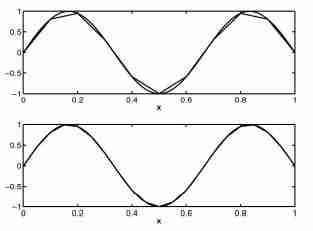
Teniamo presente che, se la funzione incognita u(x) è rappresentata da una linea continua, e noi stiamo cercando di ottenerne una soluzione approssimata $\bar u(x)$ tramite una poligonale, sarà sufficiente determinare i valori approssimati della funzione incognita nei soli punti nodali $(\bar u_h)$ che saranno poi utilizzati per definire un polinomio di grado $n-1$ che li toccherà tutti.
Le funzioni di forma interpolano la soluzione esatta fra i nodi. Siccome nel fem si vanno ad interpolare individualmente i singoli elementi che compongono la funzione da approssimare, se il numero dei nodi è n=2 allora abbiamo a che fare con una interpolazione lineare (un esempio è la interpolazione di Lagrange).
La scelta più comune e comoda, allora, è quella di prendere una base lineare fatta di triangoli (roof functions) che ha valori nulli ovunque tranne che all’interno di un elemento finito. Una base del genere è detta fungere da supporto alla funzione di forma nodale $N_h(x)$
Sia $\phi_i$ il polinomio lineare a pezzi tali che
$$\phi_i(x_j)=\left\{\begin{matrix}
1, j= i\\
0, j\neq i
\end{matrix}\right.$$
Allora la funzione $p(x)$ che si vuole interpolare si può esprimere come
$$p(x)=\sum_{i=1}^{n-1}p(x_i)\phi_i(x)$$
SISTEMA ALGEBRICO
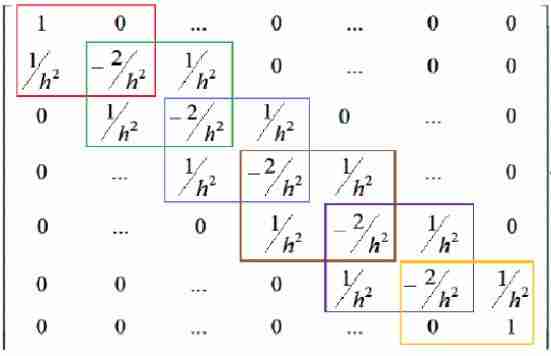
Si noti che la matrice fondamentale, oltre ad essere simmetrica, ha gli elementi non nulli sulla diagonale principale e sulle due diagonali adiacenti ovvero è tri-diagonale. Se i nodi non sono contigui non esiste un elemento comune, ovvero l’intersezione tra i due insiemi di elementi è vuota e perciò: $f_{hk}=0$.
Per una applicazione del metodo degli elementi finiti ad un problema ai valori iniziali, clicca qui.