Si consideri un reticolo di un materiale dielettrico come composto da un insieme di oscillatori armonici forzati e smorzati disaccoppiati, tutti con la stessa massa efficace $m$ e le stesse auto-frequenze $w_0$. Gli oscillatori di Lorenz sono stati impiegati per ampliare il modello semiclassico di Drude in quello che viene indicato come modello di Drude-Lorenz e datato 1905. Oggi il modello è spesso studiato a scopo educativo ed è in grado di fornire una spiegazione classica intuitiva di ciò che accade quando luce e materia interagiscono. Esso prende come riferimento un atomo i cui elettroni sono legati al nucleo come una massa può essere legata ad una più grande di circa 2000 volte, attraverso una ipotetica molla di costante elastica $k$. Gli elettroni sono particelle cariche travolte da campi elettromagnetici e sottoposte a piccole oscillazioni attorno alle posizioni di equilibrio, oscillazioni che vengono approssimate attraverso dei moti armonici di frequenza propria $\omega_0$. Oscillando gli elettroni perdono energia e re-irradiano quanto ricevuto. Il moto dell’elettrone attorno al nucleo è descritto attraverso la seconda legge di Newton:
$$m \ddot{\vec{x}}=e\vec{E}-k \vec{x} -m\gamma\dot{\vec{x}}$$
Nella forma normale utilizzata nello studio delle ODE, assai più utile ai fini di calcolo, si vede immediatamente che si ha a che fare con una equazione differenziale ordinaria di secondo ordine non omogenea
$$\ddot{\vec{x}}+\gamma\dot{\vec{x}} + \omega_0^2 \vec{x}= \frac{e\vec{E}}{\vec{x}}$$
Essa si compone di tre diversi apporti:
- un termine di deriva di interazione con il campo elettrico locale
- un termine dissipativo che descrive la perdita di energia dell’elettrone lungo il suo moto
- Un termine elastico di richiamo alla sua posizione di equilibrio
Come già accennato nell’articolo sul modello di Drude per i metalli, il dielettrico vanta il contributo di tutti e tre i termini e l’equazione va risolta nella sua interezza (nel modello di Drude per gli elettroni liberi, invece, è possibile elidere il termine elastico ). Il fisico olandese tanto osannato da Einstein e premio Nobel per la Fisica 1902, Hendrik Antoon Lorentz, propose questo modello puramente fenomenologico, per tenere conto della risposta ottica di un materiale fatto di cariche elettriche vincolate.
La gente non si rende conto di quale grande influenza abbia avuto Lorentz sullo sviluppo della fisica. Non possiamo immaginare come sarebbe andata se egli non avesse dato tanti contributi impareggiabili
Albert Einstein
Si supponga un regime sinusoidale e si esprima il campo in funzione delle componenti di Fourier
$$\vec{E(t)}= E_0(\omega) e^{i( \vec{k} \cdot \vec{r} – \omega t)}$$
Per semplicità, non si prende in considerazione il termine magnetico della forza di Lorentz e si ignora il contributo spaziale del campo: questo è vero se vale la approssimazione di dipolo e la costante reticolare $a$ è molto più piccola della lunghezza d’onda del campo $\lambda$ ($a \ll \lambda$). Allora
$$\vec{E(t)}= E_0(\omega) e^{-i \omega t}$$
ed è possibile azzardare, come tanto piace ai fisici, la forma assunta dalla soluzione
$$\vec{x(t)}= x_0(\omega) e^{-i \omega t}$$
e di conseguenza
$$\dot{\vec{x(t)}}= -i \omega x_0(\omega) e^{-i \omega t}$$
$$\ddot{\vec{x(t)}}= (-i \omega)^2 x_0(\omega) e^{-i \omega t}$$
Andando a sostituire le quantità sopra riportate, si ottiene la soluzione seguente
$$\vec{x(t)} = \frac{e\vec{E(t)}}{m} \cdot \frac{1}{\omega_0^2-\omega^2-i\omega\gamma}$$
Questo è il punto di partenza per ricavare molte grandezze utili.
POLARIZZAZIONE
Il vettore polarizzazione rappresenta il momento di dipolo per unità di volume. Supponendo che all’interno dell’unità di volume trovino posto N elettroni, il vettore $\vec{P}$ si ottiene come prodotto del numero degli elettroni per il momento di dipolo infinitesimo $\vec{p}$ di ciascun elettrone
$$\vec{P}= N\vec{p}= Ne\vec{x} = \frac{Ne^2 \vec{E}}{m} \cdot \frac{1}{\omega_0^2-\omega^2-i\omega\gamma}$$
SUSCETTIVITA’
In regime di ottica lineare vale la relazione
$$\vec{P}= \epsilon_0 \chi(\omega)\vec{E} $$
da cui è possibile ricavare l’espressione per la suscettività dividendo per la costante dielettrica del vuoto $\epsilon_0$ e il campo $\vec{E}$
$$\chi(\omega)= \frac{Ne^2}{m \epsilon_0} \cdot \frac{1}{\omega_0^2-\omega^2-i\omega\gamma} = \frac{\omega_p^2}{\omega_0^2-\omega^2-i\omega\gamma}$$
In cui abbiamo sostituito al primo termine la frequenza di plasma $\omega_p = \sqrt{\frac{Ne^2}{m \epsilon_0}}$
Caratterizzazione della funzione dielettrica complessa
La funzione dielettrica è ottenuta per mezzo della relazione:
$$\vec{D}=\epsilon_0\vec{E} + \vec{P}= \epsilon_0(1+ \chi(\omega))\vec{E} =\epsilon_0 \epsilon(\omega)\vec{E}$$ $$\epsilon(\omega) = 1 + \frac{\frac{Ne^2}{m}}{\omega_0^2-\omega^2-i\omega\gamma}$$
essendo una quantità complessa è possibile dividerla nelle due componenti: reale ed immaginaria
$$\epsilon(\omega) = \epsilon_1(\omega) +i \epsilon_2(\omega) $$
$$\epsilon(\omega) = 1 + \frac{(\omega_0^2-\omega^2)\epsilon_0 \omega_p^2}{(\omega_0^2-\omega^2)^2+\omega^2 \gamma^2} + i \frac{\omega \gamma \epsilon_0 \omega_p^2}{(\omega_0^2-\omega^2)^2+\omega^2 \gamma^2}$$
le quali danno vita a degli effetti ben distinti: la parte reale è legata a proprietà di rifrazione ed è responsabile di effetti dispersivi, mentre la parte immaginaria è legata a proprietà di assorbimento ed interviene nei processi dissipativi. SI introduca una nuova variabile nota come indice di rifrazione complesso $\tilde{n}$ tale che
$$\tilde{n} = n + i \kappa$$
con $n$ indice di rifrazione e $\kappa$ coefficiente di dispersione (o di assorbimento, talvolta indicato nei libri di testo con $\alpha$), e
$$\tilde{n}^2(\omega)\equiv \epsilon(\omega)$$
Allora
$$\left\{\begin{matrix}
\epsilon_1(\omega)= 1 – \frac{\frac{Ne^2}{m}}{\omega^2+\gamma^2} = \mathfrak{Re}(\epsilon(\omega)) = n^2(\omega) + \kappa^2(\omega)
\\
\epsilon_2(\omega)= \frac{\gamma \frac{Ne^2}{m}}{\omega(\omega^2+\gamma^2)} = \mathfrak{Im}(\epsilon(\omega)) = 2 n(\omega) \kappa(\omega)
\end{matrix}\right.$$
E’ possibile avere un idea dei diversi comportamenti analizzando il grafico seguente
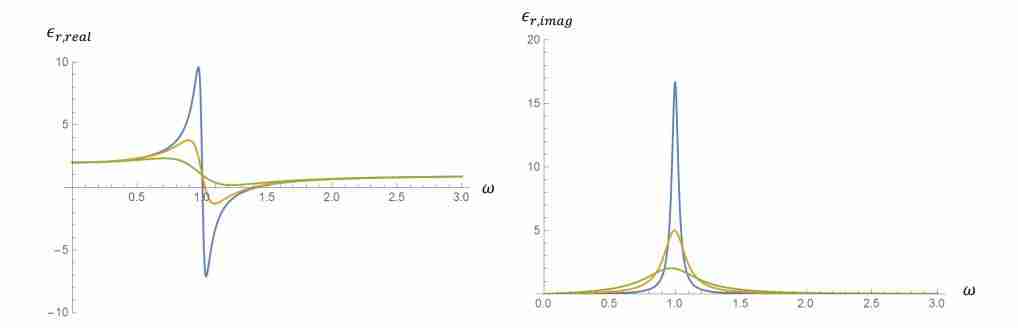
Il primo grafico rappresenta la parte reale della funzione dielettrica ovvero l’indice di rifrazione $n(\omega)$ in funzione di $\omega$, il secondo la parte complessa ovvero l’indice di assorbimento $\kappa(\omega)$ in funzione di $\omega$. In entrambi si è posto $\omega_0=1$.
$$\left\{\begin{matrix}n(\omega)= { \frac{1}{2} \{ \epsilon_1(\omega)+[\epsilon_1^2(\omega)+\epsilon_2^2(\omega)]^{\frac{1}{2}}\}}^{\frac{1}{2}}
\\
\kappa(\omega)= { \frac{1}{2} \{ – \epsilon_1(\omega)+[\epsilon_1^2(\omega)+\epsilon_2^2(\omega)]^{\frac{1}{2}}\}}^{\frac{1}{2}}\end{matrix}\right.$$
Analizzare quel che accade nei limiti a basse ed altre frequenze è utile per capire che forma assumerà la funzione graficata. A basse frequenze, ovvero per valori $\omega \rightarrow 0$:
$$\epsilon(DC) = 1 + \frac{Ne^2}{m\omega_0^2}$$
mentre ad alte frequenze per valori $\omega \rightarrow \infty$:
$$\epsilon(HF) = 1 $$
Entrambi i valori sono reali. Solo nelle regioni prossime alla risonanza, cioè per valori di $\omega \rightarrow \omega_0$ si ottiene una prova diretta della natura complessa della funzione. QUesto è esplicitato nel secondo grafico in cui la funzione è zero ovunque e diversa da zero solo per valori prossimi ad 1.
VETTORE D’ONDA E INTENSITA’ LUMINOSA
Si scrive la forma del vettore d’onda complesso a partire dall’indice di rifrazione complesso
$$\tilde{k}(\omega)=\frac{\omega }{c} \sqrt{\epsilon(\omega)}= \frac{\omega }{c}n(\omega )+i\frac{\omega }{c}\kappa(\omega )$$
Considerando solo la dipendenza spaziale dell’onda tali che
$$e^{i\tilde{k}z} = e^{i(\frac{\omega }{c}n)z} \cdot e^{-(\frac{\omega }{c}\kappa)z}$$
è possibile esprimere l’intensità luminosa come
$$I = I_0 [e^{-(\frac{\omega }{c}\kappa)z}]^2=I_0e^{-2\frac{\omega }{c}\kappa z}=I_0e^{-\frac{z}{\lambda_A}}$$
con $\lambda_A$ profondità di penetrazione o lunghezza di attenuazione
$$\lambda_A= \frac{1}{2 \kappa \frac{\omega}{c}}= \frac{\lambda}{4\pi \kappa}$$
dove si è sostituito $\omega= 2\pi \nu = \frac{2\pi}{\lambda}$. Quando arriva l’onda elettromagnetica il dielettrico viene eccitato e, a seconda della composizione della funzione dielettrica, si otterranno comportamenti diversi.