L’energia solare è una delle risorse di energia più promettenti per il futuro, valida alternativa ai combustibili fossili che, oltre a rappresentare un problema per il difficile approvvigionamento, sono destinati ad esaurirsi a breve. Ne avevamo già parlato in questo articolo: Le riserve di gas naturale nel mondo e in Italia. Ma quanta energia è in grado di fornire la nostra stella? Scopriamolo! ☀️
In copertina, foto CC by 4.0 di Alexa su Pixabay.
Le caratteristiche della radiazione solare
L’energia solare che riceviamo sulla Terra è una forma di energia elettromagnetica che viene emessa dal Sole e che si propaga nello spazio ad una velocità pari a quella della luce nel vuoto. Poiché la distanza media fra il Sole la Terra è di circa 150 milioni di km, la radiazione solare impiega circa 500 secondi (8 minuti) per raggiungere il nostro pianeta.
$$\frac{150\times 10^9}{300\times10^6}\frac{[m]}{[\frac{m}{s}]}= 500[s]$$
La radiazione solare ricopre la parte dello spettro elettromagnetico che va dall’ultravioletto all’infrarosso, con un picco di luminosità che rientra nel range del visibile, ad una lunghezza d’onda di circa 550 nm. Le stelle sono quei sistemi reali che più si approssimano ad un corpo nero e per questo la radiazione emessa dal Sole è in buon accordo con lo spettro di emissione di corpo nero posto ad una temperatura pari a quella della superficie solare, a 5777 gradi kelvin.
| Porzione dello spettro | Lunghezza d’onda | Energia | Porzione dello spettro solare |
|---|---|---|---|
| UV | 100 – 400 nm | E > 3 eV | 10% |
| VIS | 400 – 750 nm | 1.65 eV < E < 3 eV | 40% |
| IR | 750 – 2500 nm | E < 1.65 eV | 50% |
Col termine corpo nero si intende un sistema fisico ideale in grado di assorbire tutta l’energia che riceve, e che riemette radiazione solo in funzione della sua temperatura.
Origine della fonte energetica
Il Sole, come ogni stella, si trova in condizione di equilibrio idrostatico. Il collasso gravitazionale cui è sottoposto a causa della sua enorme massa, viene controbilanciato da una pressione interna di radiazione. Tale pressione è il prodotto delle reazioni nucleari che avvengono al suo interno.
Il Sole si colloca a metà della sequenza principale del diagramma di Hertzsprung-Russell come stella di categoria G2V. Ciò significa che, per le sue caratteristiche di massa, è a meta della catena protone-protone avviata 5 miliardi di anni fa. Questa, complessivamente, trasforma 4 protoni in una particella alfa (il nucleo di elio-4, composto da 2 protoni e 2 neutroni). Il processo produce 24.7 Mev di energia per singola reazione nucleare, ottenuti come difetto di massa attraverso la più famosa relazione di Einstein: $$E=mc^2$$
La costante solare
L’energia solare che arriva fino alla Terra viene espressa in termini di irradianza media, una grandezza radiometrica che identifica la potenza che incide su di un elemento di area, espressa in Watt su metro quadro. L’irradianza media che incide al di fuori della atmosfera terrestre assorbente prende il nome di costante solare $$G_0 = 1367 \frac{W}{m^2}$$
La costante solare è l’energia che incide per unità di tempo e di area su di una superficie perpendicolare alla direzione dei raggi solari, posta alla distanza di 150 milioni di km dal Sole.
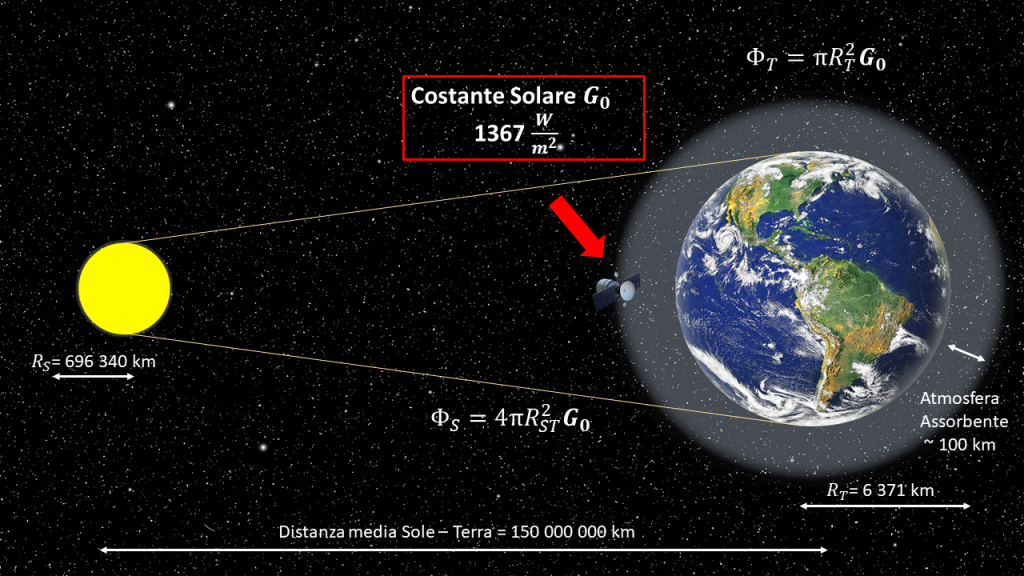
Poiché il Sole emette la radiazione in maniera isotropica, è possibile ricavare il flusso energetico totale come prodotto della costante solare per il valore della superficie della sfera che ha raggio pari alla distanza Terra-Sole.
$$\phi_S=G_0 \times 4\pi R_{ST}^2 = (1367 \frac{W}{m^2})(4\pi \cdot 150\times10^9 m)\cong 3.8\times10^{26}W$$
Human Energy Consumption
Se fosse possibile accumulare l’energia solare in arrivo, in ogni istante e in ogni punto della semisfera terrestre illuminata, si otterrebbero circa 175 000 TW di potenza. Il conto è molto veloce: è sufficiente moltiplicare la potenza per area aspecifica (la costante solare) con la proiezione della sfera terrestre sul piano di incidenza della radiazione
$$G_0 \times \pi R_T^2 = (1367 \frac{W}{m^2})(\pi \cdot 6371\times10^3 m)\cong 175\times10^{15}W$$
L’Agenzia Internazionale dell’Energia (AIE) ha stimato un consumo globale energetico pari a 50 TW. Questa unità ha poi preso il nome di HEC: human energy consumption.
$$50 TW = 1 HEC$$
In via teorica, quindi, riuscendo a collezionare tutta l’energia solare incidente sul nostro pianeta, saremmo in grado di ottenere 3500 HEC:
$$3500 HEC \times 50 TW = 175 000 TW$$