Questo articolo si riallaccia al precedente: “Perché (quasi tutti) i metalli sono grigi?“
Potete raggiungere rapidamente la risposta diretta tramite questo $\rightarrow$ Portale spaziotemporale.
La tavola periodica degli elementi è uno di quegli strumenti indispensabili di cui disporre per fornire una rapida risposta a svariati quesiti. Nel soddisfare un quesito del genere, ad esempio, si è facilitati se si hanno bene in mente le configurazioni elettroniche degli elementi coinvolti. Facciamo in modo di averla sott’occhio prima di proseguire nella lettura e ricordiamo brevemente come vengono suddivisi gli elementi che la compongono. Questi vengono suddivisi all’interno di una matrice che riporta lungo le righe il PERIODO e lungo le colonne il GRUPPO.
Il periodo rappresenta il livello di energia su cui sono disposti gli elettroni di valenza, il gruppo individua gli elementi con la stessa configurazione elettronica esterna.
Poiché il gruppo a cui appartengono gli elementi ne identifica le proprietà elettroniche e quindi la forma assunta dagli orbitali, gli elementi che si trovano lungo la stessa colonna devono avere caratteristiche simili. Ricordiamo, inoltre, che gli orbitali elettronici sono caratterizzati da diversi numeri quantici necessari per la loro identificazione.
Il numero quantico principale $n$ ne individua il livello energetico, il numero quantico di momento angolare $l$ ne individua la forma e il numero quantico di momento magnetico $m$ ne individua l’orientazione spaziale. A questi si è soliti aggiungere un quarto numero quantico detto numero quantico di spin $m_s$, che può assumere solo due valori e sta ad indicare l’orientamento del vettore di spin.
Nella tabella che segue, vengono riassunte tutte le combinazioni possibili di numeri quantici che stanno alla base della costruzione dell’atomo.
| numero quantico di momento angolare | orbitale elettronico | numero quantico magnetico | orbitali elettronici degeneri | numero massimo di elettroni posizionabili |
|---|---|---|---|---|
| l=0 | s | m=0 | 1 | 2 |
| l=1 | p | m=-1,0,1 | 3 | 6 |
| l=2 | d | m=-2,-1,0,1,2 | 5 | 10 |
| l=3 | f | m=-3,-2,-1,0,1,2,3 | 7 | 14 |
Prima di proseguire la lettura, lasciamo che il nostro cervello sia libero di trarre alcune conclusioni in autonomia: proviamo ad osservare attentamente una tavola periodica (che si può scaricare gratuitamente da questo sito) con particolare attenzione alla zona ingrandita qui di lato.
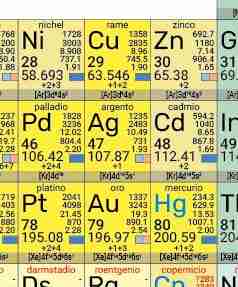
Quando il nostro cervello si trova davanti una domanda a cui non sa dare riposta diretta, è solito ricercare dei collegamenti con dei pattern a noi già noti . Come primo escamotage tenterà di trovare delle somiglianze con processi che già conosce e di cui sa motivare la soluzione. Fare mente locale è sempre una buona prassi a cui avvalersi quando si trattano nuovi argomenti: ci permette di essere critici e tutto quel che apprendiamo quando lo sappiamo contro-argomentare farà più fatica ad essere dimenticato. Di seguito per evitare di causare cefalee da lettura ho riportato nella tabella che segue, la configurazione elettronica della shell esterne degli elementi evidenziati. Questi fanno parte del gruppo degli elementi di transizione e nello specifico, appartengono ai gruppi 10, 11 e 12. I periodi di riferimento sono 4, 5 e 6. La configurazione elettronica dell’elemento considerato viene espressa prendendo come punto di partenza l’elemento nobile del periodo precedente. Questo ha tutti gli orbitali pieni che di fatto non intervengono nella formazione di nuovi legami chimici.
| gruppo 10 | gruppo 11 | gruppo 12 |
|---|---|---|
| Ni – $[Ar]3d^8 4s^2$ | Cu – $[Ar]3d^{10} 4s^1$ | Zn – $[Ar]3d^{10} 4s^2$ |
| Pd – $[Kr] 4d^{10} 5s^0$ | Ag – $[Kr] 4d^{10} 5s^1$ | Cd – $[Kr] 4d^{10} 5s^2$ |
| Pt – $[Xe] 4f^{14} 5d^9 6s^1$ | Au – $[Xe] 4f^{14} 5d^{10} 6s^1$ | Hg – $[Xe] 4f^{14} 5d^{10} 6s^2$ |
A questo punto diamo per scontato di esserci soffermati a sufficienza sulla analisi individuale di quella porzione della tavola periodica. La prima peculiarità che è possibile notare, si ha tra gli elementi del gruppo 10. La disposizione dei 10 elettroni suddivisi tra gli orbitali $d$ ed $s$ delle shell esterne, avviene diversamente per ogni elemento coinvolto. Per il gruppo 11, gli elettroni di valenza occupano prima le posizioni disponibili della shell $d$, riempiendola, e successivamente, quella della shell $s$ venendo meno alla regola valida per gli elementi di transizione per la quale la prima shell riempita dovrebbe essere la $ns$ e non la $(n-1)d$ mentre il gruppo 12 non manifesta comportamenti atipici e tutte le shell sono al completo. Come mai questa differenza di comportamento per gli elementi del gruppo del nichel?
Sulla particolarità della configurazione elettronica allo stato fondamentale del gruppo 10 del nichel
Sappiamo a sfinimento che un qualsiasi sistema fisico tende a portarsi alla sua configurazione di equilibrio o di stabilità, che corrisponde alla condizione di minor energia. Il fatto che la shell $d$ si trovi ad essere piena o quasi, coinvolge un ragionamento cui è facile accondiscendere. Spesso sentiamo dire a lezione che l’algoritmo di popolazione degli orbitali è sempre valido per elementi leggeri, e manifesta alcune eccezioni quando si trattano elementi via via più pesanti. Quando si prende in considerazione un atomo a multi-elettroni, infatti, si fanno sempre più forti le correlazioni elettroniche. Il grip tra elettroni più esterni e nucleo non è altrettanto forte quanto quello delle shell più interne (che fungono da screening per la forza di attrazione coulombiana) e diventano sempre più presenti gli effetti relativistici dovuti alle alte velocità di rotazione degli elettroni. Questi fatti, combinati tra loro, portano all’inevitabile risultato di deformare gli orbitali atomici.
Una distorsione degli orbitali coinvolge necessariamente un ri-arrangiamento della configurazione elettronica e dell’algoritmo di popolamento che si impara ai primi anni di scuola. La regola di Madelung (o la regola dell’aufbau o la regola di Hund) si mantiene valida previa qualche eccezione. Quando si ha a che fare con elementi caratterizzati da un alto numero quantico di momento angolare $l$ questo alza il livello di energia della rispettiva shell elettronica. I metalli di transizione, quindi, vedranno riempirsi prima le shell $ns$ e poi le shell $(n-1)d$ dove $n$ è il numero quantico principale che ne identifica il livello energetico.
Tuttavia, man mano che si prosegue lungo il gruppo dei metalli di transizione, questa prassi viene meno. Quando si è vicini al riempimento delle cinque shell $d$, ognuna con un sol elettrone, in qualche modo questa configurazione viene privilegiata e questo, ad esempio, fa sì che il cromo abbia configurazione elettronica $[Ar]3d^5 4s^1$ invece di $[Ar]3d^4 4s^2$. Da circa metà della transizione in poi, quando le shell $d$ dovrebbero essere semipiene, ognuna con un elettrone i cui spin sono tra loro paralleli, gli atomi si comportano in modo peculiare. Preferiscono cedere l’elettrone che si trovava nella shell sferica $s$ alla shell $d$ che si trova così ad essere completa.
- Nel periodo 4 è il rame del gruppo 11 che manifesta questo comportamento
- Nel periodo 5 è il palladio del gruppo 10 che ha la shell $d$ già piena
- Nel periodo 6 è l’oro del gruppo 11 ad avere questo comportamento. In questo caso, inoltre, compare anche la shell $f$ più interna
La contrazione dei lantanidi
Una peculiarità interessante su cui soffermarsi che non è così evidente ai nostri occhi, ma che si presenta qualora siano coinvolti gli orbitali di tipo $f$, è la contrazione dei lantanoidi che avviene per tutti gli elementi che vanno dal lantanio (elemento n.57) al lutezio (elemento n.71). Normalmente, secondo i modelli quantomeccanici che stanno alla base delle teorie atomiche gli orbitali $s$ e $p$ hanno probabilità maggiore di avere gli elettroni vicino al nucleo mentre gli orbitali $d$ ed $f$ hanno probabilità maggiore di avere gli elettroni lontano dal nucleo.
Quando si ha a che fare con elementi che presentano shell f, il raggio atomico è decisamente più piccolo di quanto previsto dalla teoria in assenza della contrazione dei lantanoidi. Questo si ripercuote su tutti gli elementi del gruppo di transizione che li seguono, uno su tutti l’oro. La causa della contrazione va ricercata nell’alta diffusione dell’orbitale f che lo rende poco efficace nello schermare l’attrazione coulombiana tra il nucleo e gli orbitali a lui più esterni ovvero gli orbitali d ed s .Una piccola percentuale di responsabilità, tuttavia, compete anche agli effetti relativistici che si fanno sempre più presenti tanto quanto più l’atomo considerato è pesante.
Un fenomeno analogo avviene per gli atomi del gruppo degli attinidi.
Effetti relativistici
Più grande è l’atomo, maggiore è il numero di protoni nel nucleo e maggiore è la attrazione coulombiana. Per evitare di cadere nel nucleo, gli elettroni sono costretti a viaggiare a velocità relativistiche, a qualche frazione di c (costante che indica la velocità della luce nel vuoto) e di conseguenza, per la stra-famosa relazione di Einstein tra massa ed energia, la massa elettronica aumenta. Tutto questo fa diminuire il raggio atomico degli elementi essendo questi determinato dalla posizione della nuvola elettronica corrispondente all’orbitale più esterno. Per la serie dei lantanidi, questo significa che è l’orbitale $6s$ a sancirne le dimensioni.
Gli orbitali s e p si contraggono verso il nucleo, portandosi ad un livello energetico più basso. Così facendo sono ancora più fortemente legati al nucleo e schermano l’attrazione coulombiana fra questi e gli orbitali più esterni. Gli orbitali d ed f, invece, si espandono allontanandosi dal nucleo, proprio perché gli orbitali più interni ne schermano la attrazione coulombiana e si portano, quindi, ad un livello di energia superiore. Così facendo complessivamente il raggio atomico cale, e la distanza energetica presente fra i vari orbitali diminuisce. Le shell s e p, e quelle f e d di avvicinano fra loro.
Questo effetto di origine decisamente relativistica è ciò cui si fa riferimento sopra quando si legge: “il numero quantico di momento angolare $l$ alza il livello di energia della rispettiva shell elettronica“.
Finora abbiamo rispolverato tantissime nozioni utili. Resta ancora insoddisfatta la domanda principale. Di tutti gli elementi metallici della tavola periodica (che sono più di 80), il nostro occhio rileva essere di colore peculiare solo il rame e l’oro. Sappiamo, tuttavia, che il comportamento chimico-fisico degli elementi di uno stesso gruppo dovrebbe essere similare. Ci aspettiamo quindi che anche l’argento debba apparirci di colore diverso, ma così non è. Vedremo in realtà che anche questo elemento manifesta le stesse caratteristiche di rame ed oro solo che noi non siamo in grado di rivelarlo visivamente.
Il modello di Lorentz
Andiamo più al dettaglio e nel farlo, teniamo bene a mente la funzione dielettrica complessa, che contiene tutte le informazioni utili a rispondere a questa domanda. Ne avevamo già parlato in questo articolo sul modello di Drude-Lorentz che funge da ottimo punto di partenza. Siano $\epsilon(\omega)$ la funzione dielettrica complessa che tiene conto delle proprietà ottiche dei metalli, $\epsilon_0$ la costante dielettrica del vuoto
$$\epsilon_0 = 8,854 187 8128(13) \cdot 10^{-12} \frac{C^2}{N \cdot m^2}$$
e $\epsilon_r(\omega)$ la funzione dielettrica relativa data dal prodotto fra le due: $\epsilon_r(\omega)= \epsilon_0 \cdot \epsilon(\omega)$. Sappiamo che gli elettroni di conduzione sono liberi di muoversi per tutto il metallo, e che sono possibili transizioni di inter-banda (fra bande separate da un gap energetico) se l’energia dei fotoni incidenti è superiore a quella del gap di banda. Si considerino quindi, separatamente, i diversi contributi elettronici che portano alla formazione della funzione dielettrica relativa $\epsilon_r(\omega)$
$$\epsilon_r(\omega)= \epsilon_r(\omega)^{free \ e^-} + \epsilon_r(\omega)^{bound \ e^-}$$
- dove il primo termine $\epsilon_r(\omega)^{free \ e^-} $ indica il contributo dovuto agli elettroni liberi responsabili delle transizioni intra-banda, quelle cioè che avvengono fra gli stati al livello di Fermi in bande non completamente piene. La trattazione corretta per questo tipi di elettroni è quella del modello di Drude:
$$\epsilon_r(\omega)^{free \ e^-} = 1 – \frac{\omega_P^2}{\omega^2 + i\omega \gamma}$$
con $\omega_P$ frequenza di plasma del volume (bulk) e $\omega$ frequenza del campo elettrico applicato - mentre il secondo termine $\epsilon_r(\omega)^{bound \ e^-}$ indica il contributo degli elettroni legati responsabili delle transizioni inter-banda, quelle che avvengono tra stati separati da un gap energetico. La trattazione corretta per questo genere di elettroni è quella del modello di Lorentz che coinvolge anche un termine di forza elastica di richiamo:
$$\epsilon_r(\omega)^{bound \ e^-} = 1 + \frac{\omega_p^2}{\omega_0^2-\omega^2 – i\omega \gamma}$$
con $\omega_p$ frequenza di plasma, $\omega$ frequenza del campo elettrico applicato e $\omega_0$ frequenza propria degli elettroni intesi come insiemi di oscillatori attratti dal nucleo
A causa della presenza del gap, i contributi inter-banda si rilevano solo ad alte energie, solitamente vicino al range ultravioletto, mentre quelli intra-banda si verificano con fotoni poco energetici e coinvolgono gli elettroni liberi al livello di Fermi. Tenendo bene a mente quanto visto negli articoli sui due modelli di Drude e Lorentz linkati sopra, si considerino solo gli effetti del gas di elettroni liberi e si decomponga $\epsilon_r(\omega)$ nelle due parti reale ed immaginaria
$$\epsilon_r(\omega)^{free \ e^-} = 1 – \frac{\omega_P^2}{\omega^2 + \gamma^2} +i \frac{\gamma \omega_P^2}{\omega(\omega^2 + \gamma^2)}$$
quel che si ottiene applicando il modello all’oro, è un grafico di questo tipo
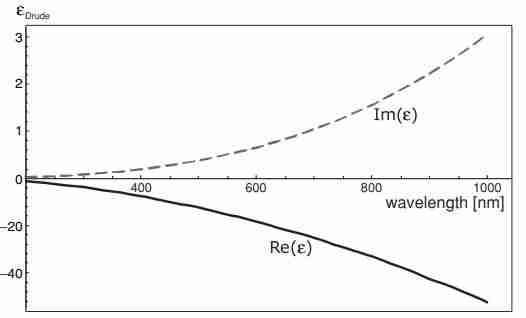
Andamento della funzione dielettrica per l’oro secondo il modello ad elettroni liberi di Drude in cui siamo andati a sostituire i seguenti valori: $\omega_P=13,8 \cdot 10^{15} s^{-1}$ e $\gamma = 1,075 \cdot 10{14} s^{-1}$. Da notare, in particolare, le diverse scale che competono alla parte reale ed immaginaria della funzione dielettrica.
Ricordando che la parte reale della funzione dielettrica è legata all’indice di rifrazione della materiale $\mathfrak{Re}(\epsilon(\omega)) = n^2(\omega)$ e che la parte complessa della funzione dielettrica è legata all’indice di dispersione (o assorbimento) dello stesso $\mathfrak{Im}(\epsilon(\omega)) = n^2(\omega)$ possiamo intuire che un valore alto e negativo per $\epsilon(\omega)$ è sintomo di forte assorbimento per cui la radiazione sarà in grado di penetrare solo i layers più superficiali del materiale.
I risultati così ottenuti non sono in linea con quanto atteso per l’oro. Un colore giallastro sta ad indicare un forte assorbimento della porzione bluastra e una forte riflessione della porzione giallognola dello spettro del visibile. Evidentemente il modello di Drude per i metalli non è sufficiente a giustificare un tale fenomeno. Proviamo ad applicare il modello di Lorentz valido per i materiali dielettrici, alla controparte vincolata degli elettroni del metallo.
Si considerino quindi solo gli effetti degli elettroni di bulk vincolati e si decomponga $\epsilon_r(\omega)$ nelle due parti reale ed immaginaria
$$\epsilon_r(\omega)^{bound \ e^-} = 1 + \frac{\omega_p^2(\omega_0^2- \omega^2)}{(\omega_0^2- \omega^2)^2 + \gamma^2 \omega^2} + i \frac{\gamma \omega_p^2 \omega}{(\omega_0^2- \omega^2)^2 + \gamma^2 \omega^2} $$
Ciò che si ottiene è più in linea con la realtà dei fatti. Il colore giallastro dell’oro puro è ben giustificato dal comportamento risonante che si ottiene se si considerano gli elettroni vincolati del materiale come degli oscillatori di Lorentz.
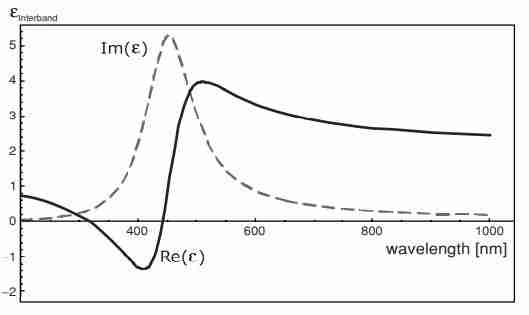
Andamento della funzione dielettrica per l’oro secondo il modello di Lorentz applicato agli elettroni vincolati. In questo caso siamo andati a sostituire i seguenti valori: $\omega_p=45 \cdot 10^{14} s^{-1}$, $\gamma = 9 \cdot 10{14} s^{-1}$ e $\omega_0= \frac{2 \pi c}{\lambda}$ con $\lambda= 450 nm$ . Da notare, oltre alla diversa forma assunta dalla funzione dielettrica, uno scaling più omogeneo fra la parte reale ed immaginaria di $\epsilon(\omega)$.
La parte immaginaria della funzione dielettrica, legata ai fenomeni dispersivi, mostra un andamento risonante; ciò accade nella prima metà dello spettro. In particolare, l’oro assorbe fortemente il blu e il verde con un picco di massimo ai $450 \ nm$ pari ad una energia di $2,75 \ eV$ mentre riflette la parte che va dai 600 nm in su. E’ stato necessario applicare il modello di Lorentz agli elettroni di bulk per un materiale metallico come l’oro. Lo stesso può dirsi anche per rame ed argento che assorbono rispettivamente a $2,1 eV$ e $3,1 eV$.
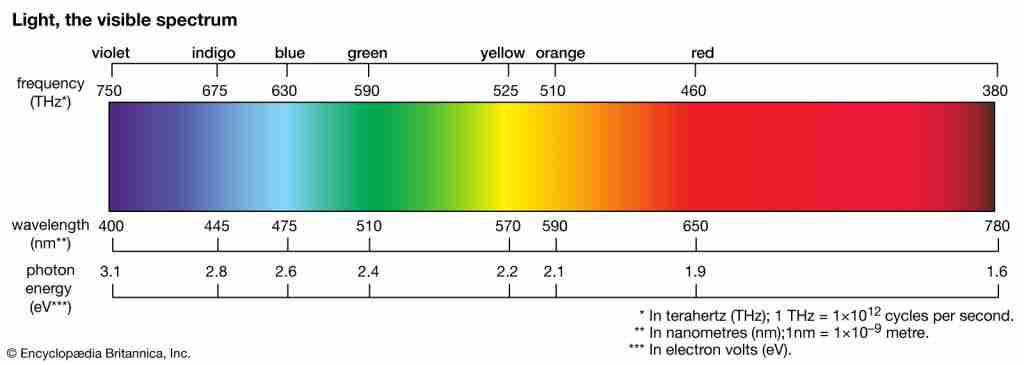
Transizioni interbanda e polaritoni plasmonici di superficie
Le vetrate colorate delle grandi cattedrali costruite a partire dal medioevo, sono caratterizzate dall’essere composte da soluzioni colloidali in cui sono presenti di nanoparticelle d’oro di diverse dimensioni. Ciò da luogo a tantissimi colori differenti: rosso, blu, verde, giallo ecc.. Per saperne di più su come sia possibile ottenere una gamma così vasta di colori a partire dall’oro, vi rimando a questo articolo.
Perché il rame, l’oro e teoricamente anche l’argento non sono grigi
Ora disponiamo di tutti gli strumenti necessari per rispondere alla domanda. Abbiamo visto che la configurazione elettronica dei tre metalli nobili è la stessa e rappresentano eccezioni alla regola di Madelung. Tuttavia le loro proprietà ottiche risultano essere differenti. Quando un atomo viene irradiato da una sorgente non polarizzata, esso assorbe quella porzione dello spettro elettromagnetico compatibile con il gap energetico degli orbitali tra cui avviene una transizione. L’atomo continuerà ad assorbire quella componente per mantenere l’elettrone eccitato nella sua nuova posizione.
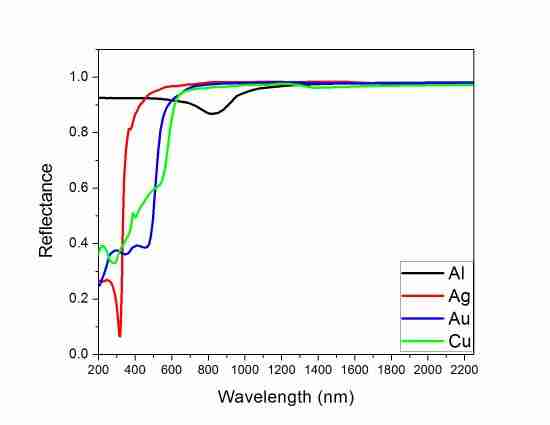
Spettro di riflettanza di alcuni metalli in funzione della loro lunghezza d’onda.
Una volta che la sorgente viene meno, esso riemette l’energia ricevuta sotto forma di radiazione elettromagnetica. Le transizioni ottiche responsabili dell’assorbimento per i tre metalli avvengono fra le stesse shell ma a livelli energetici diversi. Normalmente le transizioni atomiche avvengono nei range del visibile e dell’UV ma nella maggior parte dei metalli, le transizioni atomiche avvengono solo nell’UV ovvero ad energie più alte e non visibili ad occhio umano. I nostri occhi sono sensibili solo alla componente visibile della radiazione. Di regola i metalli non assorbono in questa porzione dello spettro e riflettono la radiazione incidente. Per questo ci appaiono di color grigiastro. Inoltre, diversamente dalla maggior parte degli oggetti che conosciamo che riflettono diffusamente, ovvero ad angoli casuali, i metalli lo fanno specularmente, cioè ad angoli di riflessione coincidenti a quelli di incidenza, per cui ci appaiono lucidi.
| metallo | differenza energetica fra le shell d ed s (eV) | range di massimo assorbimento (nm) | colore percepito |
|---|---|---|---|
| oro (Au) | 1.9 | dal vicino UV fino a 400 | giallo brillante |
| rame (Cu) | 2.7 | dal vicino UV fino a 500 | marrone tendente al rosso |
| argento (Ag) | 4.8 | 300 (vicino UV) | grigio metallico |
Normalmente i metalli sono opachi a tutte le frequenze d’onda escluse quelle più energetiche a partire dagli UV. Infatti, a partire dagli UV in poi diventano trasparenti. Nell’argento (Ag) di numero atomico 47 è la transizione $4d \rightarrow 5s$ ad assegnarne il colore. La distanza fra i livelli energetici è sufficiente a far ricadere la transizione nell’ultravioletto. Nonostante la transizione elettronica sia la stessa degli unici metalli colorati, esso ci appare come tutti gli alti. Solo se i nostri occhi fossero sensibili al range UV lo vedremmo diverso.
Nel rame (Cu) di numero atomico 29 è la transizione $3d \rightarrow 4s$ che ne assegna il colore. Il gap energetico di $2.7 eV$ richiesto alla transizione ricade nella parte più energetica del visibile. Assorbendo queste energie, ciò che re-irradia manca della componente verde e, di conseguenza, appare rossiccio. Nell’oro (Au), invece, di numero atomico 79, intervengono effetti relativistici. Come abbiamo visto sono dovuti al fatto che l’atomo è abbastanza pesante. Gli elettroni sono soggetti a una più intensa attrazione elettrostatica. L’energia della shell $5d$ aumenta mentre quella della shell $6s$ diminuisce. L’energia richiesta alla transizione è inferiore rispetto a quella dell’argento perché i due orbitali si avvicinano tra loro, e ciò conduce ad uno shift dall’ultravioletto al primo range visibile nello spettro di assorbimento. Di conseguenza quando illuminato da luce non polarizzata, l’oro riflette tuto lo spettro che riceve ad esclusione della componente blu e ci appare, appunto, color oro.